
 如图,已知⊙P的半径是1,圆心P在抛物线y=(x-2)2上运动,且⊙P与坐标轴相切时,满足题意的⊙P有几个.( )
如图,已知⊙P的半径是1,圆心P在抛物线y=(x-2)2上运动,且⊙P与坐标轴相切时,满足题意的⊙P有几个.( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①和x轴相切,②和y轴相切,求出纵坐标和横坐标,即可得出选项.
解答 解:①和x轴相切,
∵则半径为1的⊙P与x轴相切,
∴P的纵坐标为:±1,
若P的纵坐标为1,则1=(x-2)2,
解得:x1=3,x2=1,
∴点P的坐标为:(,3,1)或(1,1);
若P的纵坐标为-1,-1=(x-2)2,
此时方程无解;
②和y轴相切,
∵则半径为1的⊙P与y轴相切,
∴P的横坐标为:±1,
若P的横坐标为1,则y=1,即点的坐标为(1,1),
若P的横坐标为-1,则y=(-1-2)2=9,即点的坐标为(-1,9),
所以有3个不同的点,
故选C.
点评 此题考查了切线的性质以及二次函数的图象上点的性质.注意根据题意得到P的纵坐标或横坐标为±1是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
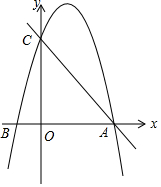 已知抛物线y=-x2+mx+m+1与x轴交于A、B两点(A在B点的右侧),与y轴交于点C.
已知抛物线y=-x2+mx+m+1与x轴交于A、B两点(A在B点的右侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | abc | C. | 1000a+10b+c | D. | 100c+10b+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com