
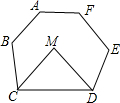
 如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
分析 首先求得六边形的内角和,则∠BCD与∠CDE的和即可求得,然后根据角平分线的定义求得∠MCD+∠MDC,然后在△MCD中利用三角形内角和定理求解.
解答 解:六边形的内角和是:(6-2)×180°=720°,
则∠BCD+∠CDE=720°-(∠A+∠B+∠E+∠F)=720°-510°=210°,
∵CM,DM分别平分∠BCD和∠CDE,
∴∠MCD+∠MDC=$\frac{1}{2}$(∠BCD+∠CDE)=$\frac{1}{2}$×210°=105°,
在△MCD中,∠M=180°-(∠MCD+∠MDC)180°-105°=75°.
故选C.
点评 本题考查了多边形的内角和定理,以及角平分线的定义,正确求得∠MCD+∠MDC是关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
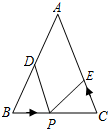 如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.查看答案和解析>>
科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:填空题
把命题“等角的余角相等”改写成“如果……,那么……”的形式是_______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com