
分析 利用根与系数的关系及一元二次方程的解的定义得出m+n=-2,m•n=-5,m2=5-2m,再将m2+3mn+n2,m2-mn+3m+n变形为两根之积或两根之和的形式,然后代入数值计算即可.
解答 解:∵m、n是方程x2+2x-5=0的两个实数根,
∴mn=-5,m+n=-2,m2+2m-5=0,
∴m2=5-2m,
∴m2+3mn+n2=(m+n)2+mn=4-5=-1,
∴m2-mn+3m+n
=(5-2m)-(-5)+3m+n
=10+m+n
=10-2
=8.
故答案为:-1,8.
点评 此题主要考查了根与系数的关系及一元二次方程的解的定义,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
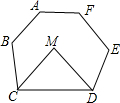 如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com