
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
【答案】
(1)
解:∵AD∥BC,∠A=70°.
∴∠ ABC=180°-∠ A=110°.
∵BE平分∠ABC.
∴∠ABE= ![]() ∠ABC=55°.
∠ABC=55°.
(2)
证明:DF∥BE,理由如下:
∵AB∥ CD.
∴∠A+∠ADC=180°,∠2=∠AFD.
∵AD∥ BC.
∴∠A+∠ABC=180°.
∴∠ADC=∠ABC.
∵∠1=∠2= ![]() ∠ADC,∠ABE=
∠ADC,∠ABE= ![]() ∠ABC.
∠ABC.
∴∠2=∠ABE.
∴∠AFD =∠ABE.
∴DF∥BE.
【解析】(1)由平行线的性质可求得∠ ABC =110°,由角平分线的定义可求得∠ABE= ![]() ∠ABC=55°;
∠ABC=55°;
(2)DF∥BE,理由:由AB∥ CD,根据平行线的性质可得∠A+∠ADC=180°,∠2=∠AFD,再由AD∥ BC,根据平行线的性质可得
∠A+∠ABC=180°,所以∠ADC=∠ABC,再由∠1=∠2= ![]() ∠ADC,∠ABE=
∠ADC,∠ABE= ![]() ∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
【考点精析】利用角的平分线和平行线的判定与性质对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】抽查了某校在六月份里5天的日用电量,结果如下:
400 410 395 405 390(单位;度)
根据以上数据,估算该校六月份的总用电量是(单位;度)( )
A. 12400 B. 12000 C. 2000 D. 400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD>AB,AE是∠BAC的平分线交BC于点E,以AC上一点O 为圆心作圆,使 ⊙O经过A,E两点,⊙O交AC于点F,
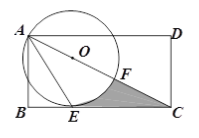
(1)求证:BC是⊙O的切线;
(2)若AB=3,∠BAC=60°,试求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.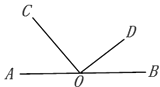
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列解方程中正确的有
① ![]() x+4=﹣3,解得x=﹣
x+4=﹣3,解得x=﹣ ![]()
②3x﹣5=7x,解得x= ![]()
③﹣(x﹣1)=﹣ ![]() (x+1),解得x=3
(x+1),解得x=3
④ ![]() ﹣
﹣ ![]() =
= ![]() ,解得x=﹣8.
,解得x=﹣8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5 ![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点. 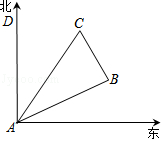
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用大小相等的小正方形(阴影部分)按一定规律拼成下列图形,拼成第1个图形需要2个小正方形,拼第2个图形需要6个小正方形,拼第3个图形需要12个小正方形……那么第5个图形中需要小正方形个, 第n个图形中需要小正方形个.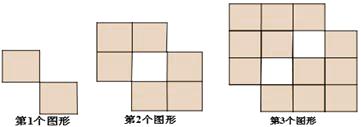
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,不正确的是( )
A. 菱形的四条边相等
B. 对角线相等的平行四边形是矩形
C. 平行四边形邻边相等
D. 正方形对角线相等且互相垂直平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com