
分析 首先求出$\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$的值是多少;然后根据($\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$)•ω=1,用1除以$\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$的值,求出ω的值是多少即可.
解答 解:∵a≠±2,
∴$\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$
=$\frac{4}{{a}^{2}-4}$-$\frac{a+2}{{a}^{2}-4}$
=$\frac{2-a}{{a}^{2}-4}$
=-$\frac{1}{a+2}$
∵($\frac{4}{{a}^{2}-4}$+$\frac{1}{2-a}$)•ω=1,
∴ω=1÷(-$\frac{1}{a+2}$)=-a-2.
点评 此题主要考查了分式的混合运算,要熟练掌握,(1)注意运算顺序:分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.(2)注意化简结果:运算的结果要化成最简分式或整式.分子、分母中有公因式的要进行约分化为最简分式或整式.(3)注意运算律的应用:分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律运算,会简化运算过程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -(3x+2)=-3x+2 | B. | -(-2x-7)=-2x+7 | C. | -(5x-6)=6-5x | D. | -(-2x-7)=2x-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
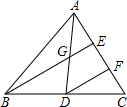 如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<0且ac≥1 | B. | a>0且ac≥1 | C. | a>0且ac>1 | D. | a<0且ac>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com