科目：初中数学 来源：[首发]广东省深圳市南山区2017届九年级第三次模拟考试数学试卷 题型：单选题
数据
，
，，
的众数有两个，则这组数据的中位数是( )．
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目：初中数学 来源：辽宁省盘锦市2017年中考三模数学试卷 题型：解答题
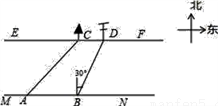
在综合实践课上，小聪所在小组要测量一条河的宽度，如图，河岸EF∥MN，小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向，然后沿河岸走了30米，到达B处，测得河对岸电线杆D位于北偏东30°方向，此时，其他同学测得CD=10米．请根据这些数据求出河的宽度．（精确到0.1）（参考数据：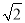 
≈1.414， 
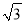≈1.132）
查看答案和解析>>
科目：初中数学 来源：辽宁省盘锦市2017年中考三模数学试卷 题型：填空题
如图，一次函数
的图象与反比例函数
的图象相交于A、B两点，当y1>y2时，－1<x<0或x>3，则一次函数的解析式为_____________________.
查看答案和解析>>
科目：初中数学 来源：辽宁省盘锦市2017年中考三模数学试卷 题型：单选题
如图，在平面直角坐标系中，点P（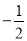
，a）在直线y=2x+2与直线y=2x+4之间，则a的取值范围是（ ）
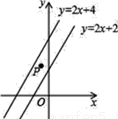
A. 2＜a＜4 B. 1＜a＜3 C. 1＜a＜2 D. 0＜a＜2
查看答案和解析>>
科目：初中数学 来源：2017年北京怀柔初三数学二模试卷及答案 题型：解答题
在△ABN中，∠B =90°，点M是AB上的动点（不与A,B两点重合），点C是BN延长线上的动点（不与点N重合），且AM=BC，CN=BM，连接CM与AN交于点P.
（1）在图1中依题意补全图形;
（2）小伟通过观察、实验，提出猜想:在点M，N运动的过程中，始终有∠APM=45°.?小伟把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的一种思路:
要想解决这个问题，首先应想办法移动部分等线段构造全等三角形，证明线段相等，再构造平行四边形，证明线段相等，进而证明等腰直角三角形，出现45°的角，再通过平行四边形对边平行的性质，证明∠APM=45°.
他们的一种作法是：过点M在AB下方作MD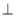
AB于点M,并且使MD=CN.通过证明△AMD
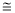△CBM,得到AD=CM,再连接DN，证明四边形CMDN是平行四边形，得到DN=CM，进而证明△ADN是等腰直角三角形，得到∠DNA=45°.又由四边形CMDN是平行四边形，推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路，用另一种方法证明∠APM=45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的整数解是_______________ .
，则
__________．
﹣（
﹣
）-