
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

【答案】(1)6;(2)10或![]() ;
;
【解析】
(1)根据图象变化确定a秒时,P点位置,利用面积求a;
(2)P、Q两点的函数关系式都是在运动6秒的基础上得到的,因此注意在总时间内减去6秒;
(3)以(2)为基础可知,两个点相距3cm分为相遇前相距或相遇后相距,因此由(2)可列方程.
(1)由图象可知,当点P在BC上运动时,△APD的面积保持不变,则a秒时,点P在AB上.
![]() ,
,
∴AP=6,
则a=6;
(2)由(1)6秒后点P变速,则点P已行的路程为y1=6+2(x﹣6)=2x﹣6,
∵Q点路程总长为34cm,第6秒时已经走12cm,
故点Q还剩的路程为y2=34﹣12﹣![]() ;
;
(3)当P、Q两点相遇前相距3cm时,
![]() ﹣(2x﹣6)=3,解得x=10,
﹣(2x﹣6)=3,解得x=10,
当P、Q两点相遇后相距3cm时,
(2x﹣6)﹣(![]() )=3,解得x=
)=3,解得x=![]() ,
,
∴当x=10或![]() 时,P、Q两点相距3cm
时,P、Q两点相距3cm


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】水蜜桃是无锡市阳山的特色水果,水蜜桃一上市,水果店的老板用2000元购进一批水密桃,很快售完;老板又用3300元购进第二批水蜜桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批水蜜桃每件进价是多少元?
(2)老板以每件65元的价格销售第二批水蜜桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批水密桃的销售利润不少于288元,剩余的仙桃每件售价最多打几折?(利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴当a=b=1时,M有最小值1
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
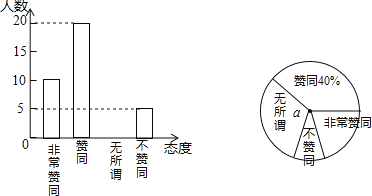
(1)在这次问卷调查中,一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 °;
(4)若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 .(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
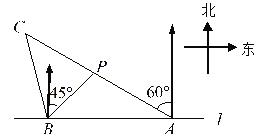
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com