

分析 探究(一):如图1在⊙O上任取一点C(不为点A、B),连接PC、OC,证得PA<PC即可得到PA是点P到⊙O上的点的最短距离;图2中有圆,找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可;
探究(二)根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可;
探究(三)由题意易证△ADE≌△DCF,从而得到AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.
解答 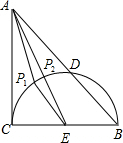 解:(1)找到BC的中点E,连接AE,交半圆于P2,在半圆上任取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值.
解:(1)找到BC的中点E,连接AE,交半圆于P2,在半圆上任取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值.
在Rt△ABC中,∠ACB=90°,AC=BC=2,CE=$\frac{1}{2}$BC=1
∴AE=$\sqrt{A{C}^{2}+C{E}^{2}}=\sqrt{5}$,
∵P2E=1,
∴AP2=$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1.
(2)如图所示:因为点M是AD的中点,
∴AM=MA′=$\frac{1}{2}$AD=1,
由于△AMN沿MN所在的直线翻折得到△A′MN
∴MA′=AM=1是定值,当点A′在MC上时,A′C长度最小.
过点M作ME⊥DC于点E,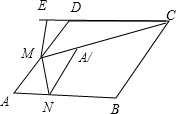
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠EDM=60°,
∴∠EMD=30°,
∴ED=$\frac{1}{2}$MD=$\frac{1}{2}$,
∴EM=DM×cos30°=$\frac{\sqrt{3}}{2}$,
∴MC=$\sqrt{E{M}^{2}+E{C}^{2}}$=$\sqrt{7}$,
∴A′C=MC-MA′=$\sqrt{7}-1$.
答:A′C长度的最小值为$\sqrt{7}-1$.
(3)∵四边形ABCD是正方形,
∴AD=DC=4,∠ADC=∠C=90°.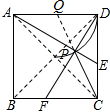 在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠C}\\{DE=CF}\end{array}\right.$,
在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠C}\\{DE=CF}\end{array}\right.$,
∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°.
∴AE⊥DF;
由于点P在运动中保持∠APD=90°,
∴点P的路径是一段以AD为直径的弧,
设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
在Rt△QDC中,QC=$\sqrt{C{D}^{2}+Q{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴CP=QC-QP=2$\sqrt{5}$-2.
答:线段CP的最小值为2$\sqrt{5}$-2.
点评 本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系及圆的性质,知道线段最短时点的位置并能确定出最小时点的位置是解题关键,也是本题的难点.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
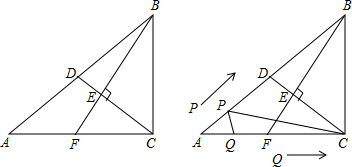 如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8.D是斜边AB的中点,BF⊥CD于点E,交AC于点F.
如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8.D是斜边AB的中点,BF⊥CD于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
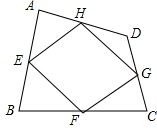 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用某种建材,利用互相垂直的两面围墙,围成一个由三块矩形组成的菜园(如图),若建材的总长度为60米,问矩形的宽x为多少时,菜园的面积最大,最大面积是多少?
用某种建材,利用互相垂直的两面围墙,围成一个由三块矩形组成的菜园(如图),若建材的总长度为60米,问矩形的宽x为多少时,菜园的面积最大,最大面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com