
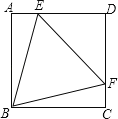
【题目】如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
①DE=DF;②∠AEB=75°;③BE=![]() DE;④AE+FC=EF.
DE;④AE+FC=EF.
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据等腰直角三角形的性质可判断③的正误;根据线段垂直平分线的知识可以判断④的正误.
解:∵四边形ABCD是正方形,∴AB=BC,∵△BEF是等边三角形,∴BBF,∵在Rt△ABE和Rt△BCF中,AB=BC,BE=BF,∴Rt△ABE≌△BCF(HL)∴AE=CF,AD=DC,AD-AE=CD-CF,
∴DE=DF,∴①正确;
∵DE=DF,∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠BEF=60°,∴∠AEB=75°,∴②正确;
∵BE=EF=![]() DE,∴③正确;
DE,∴③正确;
如图,连接BD,交EF于G点,
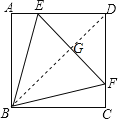
∴BD⊥EF,且BD平分EF,∵∠CBD≠∠DBF,∴CF≠FG,∴AE+FC≠EF,∴④错误;
故选C.
“点睛”本题考查了全等三角形的判定和性质,正方形的性质,等边三角形的性质,考本题中 求值△ABE≌△BCF是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,E点为BC中点,连接AE,过B点作BF⊥AE,交CD于F点,交AE于G点,连接GD,过A点作AH⊥GD交GD于H点.
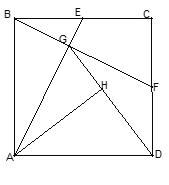
(1) 求证:△ABE≌△BCF;
(2) 若正方形边长为4,AH=![]() ,求△AGD的面积.
,求△AGD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】年初,工信部官网发布了2016年通信运营业统计公报,数据显示,2016年,4G用户数呈爆发式增长,全年新增3.4亿户,总数达到770 000 000亿户,将770 000 000用科学记数法表示应为( )
A.0.77×109
B.7.7×107
C.7.7×108
D.7.7×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2015~2017)》,某市政府决定2015年投入6000万元用于改善医疗卫生服务,比2014年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2015年投入“需方”的资金将比2014年提高30%,投入“供方”的资金将比2014年提高20%.
(1)该市政府2014年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2015年投入“需方”和“供方”的资金是多少万元?
(3)该市政府预计2017年将有7260万元投入改善医疗卫生服务,若从2015~2017年每年的资金投入按相同的增长率递增,求2015~2017年的年增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com