
【题目】正方形ABCD中,E点为BC中点,连接AE,过B点作BF⊥AE,交CD于F点,交AE于G点,连接GD,过A点作AH⊥GD交GD于H点.
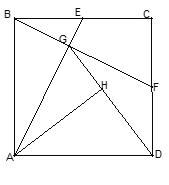
(1) 求证:△ABE≌△BCF;
(2) 若正方形边长为4,AH=![]() ,求△AGD的面积.
,求△AGD的面积.
【答案】(1)见解析(2)![]()
【解析】(1)易得∠1=∠3,这两个三角形中都有一个角是直角,加上正方形的边长相等,利用角边角可得这两个三角形全等;
(2)求得DG的长就可以求得△AGD的面积.易得F为CD的中点,延长BF交AD的延长线于点M,可构造出△BCF≌△MDF,那么可得DM=BC=AD,就可以求得GD的长,也就求得了△AGD的面积.
解:证明:(1)正方形ABCD中,∠ABE=90°,∴∠1+∠2=90°,
又AE⊥BF,∴∠3+∠2=90°,则∠1=∠3,
又∵四边形ABCD为正方形,
∴∠ABE=∠BCF=90°,AB=BC
在△ABE和△BCF中,
∠1=∠3,AB=BC,∠ABE=∠BCF,∴△ABE≌△BCF(ASA)
(2)延长BF交AD延长线于M点,
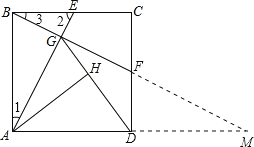
∴∠MDF=90°
由(1)知△ABE≌△BCF,
∴CF=BE
∵E点是BC中点,
∴BE=![]() BC,即CF=
BC,即CF=![]() CD=FD,
CD=FD,
在△BCF和△MDF中,
∠BCF=∠MDF,CF=DF,∠BFC=∠MFD,
∴△BCF≌△MDF(ASA)
∴BC=DM,即DM=AD,D是AM中点
又AG⊥GM,即△AGM为直角三角形,
∴GD=![]() AM=AD
AM=AD
又∵正方形边长为4,
∴GD=4
S△AGD=![]() GDAH=
GDAH=![]() ×4×
×4×![]() =
=![]() .
.
“点睛”综合考查了正方形的性质与全等三角形的判定与性质;利用正方形一边的中点构造全等三角形是常用的辅助线方法,是解决本题的难点.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2.
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】明代珠算大师程大位著有《珠算统宗》一书,有下面的一道题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤(1斤等于16两)”.据此可知,客有______人,银有______两.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:
①DE=DF;②∠AEB=75°;③BE=![]() DE;④AE+FC=EF.
DE;④AE+FC=EF.
其中正确的结论个数有( )
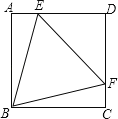
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
(1)设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为 米;
(2)若此时花圃的面积刚好为45m2,求此时花圃的长与宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,其中,参加书法兴趣小组的有8人,文学兴趣小组的有11人,舞蹈兴趣小组的有9人,其余参加绘画兴趣小组.则参加绘画兴趣小组的频率是( )
A.0.1
B.0.15
C.0.25
D.0.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列分解因式的过程:
x2+2ax﹣3a2
=x2+2ax+a2﹣a2﹣3a2(先加上a2,再减去a2)
=(x+a)2﹣4a2(运用完全平方公式)
=(x+a+2a)(x+a﹣2a )(运用平方差公式)
=(x+3a)(x﹣a)
像上面那样通过加减项配出完全平方式后再把二次三项式分解因式的方法,叫做配方法.
请你用配方法分解因式:m2﹣4mn+3n2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是________________.
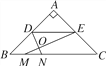
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com