
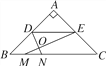
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是________________.
【答案】![]() 或
或![]()
【解析】由图可知,在△OMN中,∠OMN的度数是一个定值,且∠OMN不为直角. 故当∠ONM=90°或∠MON=90°时,△OMN是直角三角形. 因此,本题需要按以下两种情况分别求解.
(1) 当∠ONM=90°时,则DN⊥BC.
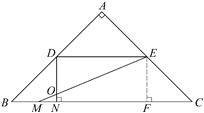
过点E作EF⊥BC,垂足为F.(如图)
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠C=45°,
∵BC=20,
∴在Rt△ABC中,![]() ,
,
∵DE是△ABC的中位线,
∴![]() ,
,
∴在Rt△CFE中,![]() ,
,![]() .
.
∵BM=3,BC=20,FC=5,
∴MF=BC-BM-FC=20-3-5=12.
∵EF=5,MF=12,
∴在Rt△MFE中,![]() ,
,
∵DE是△ABC的中位线,BC=20,
∴![]() ,DE∥BC,
,DE∥BC,
∴∠DEM=∠EMF,即∠DEO=∠EMF,
∴![]() ,
,
∴在Rt△ODE中,![]() .
.
(2) 当∠MON=90°时,则DN⊥ME.
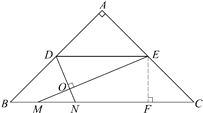
过点E作EF⊥BC,垂足为F.(如图)
∵EF=5,MF=12,
∴在Rt△MFE中,![]() ,
,
∴在Rt△MFE中,![]() ,
,
∵∠DEO=∠EMF,
∴![]() ,
,
∵DE=10,
∴在Rt△DOE中,![]() .
.
综上所述,DO的长是![]() 或
或![]() .
.
故本题应填写:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD中,E点为BC中点,连接AE,过B点作BF⊥AE,交CD于F点,交AE于G点,连接GD,过A点作AH⊥GD交GD于H点.
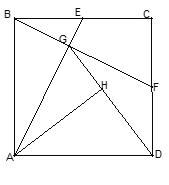
(1) 求证:△ABE≌△BCF;
(2) 若正方形边长为4,AH=![]() ,求△AGD的面积.
,求△AGD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
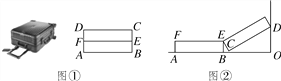
【题目】如图①所示的旅行箱的箱盖和箱底两部分的厚度相同,四边形ABCD为形如矩形的旅行箱一侧的示意图,F为AD的中点,EF∥CD.现将放置在地面上的箱子打开,使箱盖的一端点D靠在墙上,O为墙角,图②为箱子打开后的示意图.箱子厚度AD=30cm,宽度AB=50cm.
(1)图②中,EC=________cm,当点D与点O重合时,AO的长为________cm;
(2)若∠CDO=60°,求AO的长(结果取整数值,参考数据:sin60°≈0.87,cos60°=0.5,tan60°≈1.73,可使用科学计算器).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2015~2017)》,某市政府决定2015年投入6000万元用于改善医疗卫生服务,比2014年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2015年投入“需方”的资金将比2014年提高30%,投入“供方”的资金将比2014年提高20%.
(1)该市政府2014年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2015年投入“需方”和“供方”的资金是多少万元?
(3)该市政府预计2017年将有7260万元投入改善医疗卫生服务,若从2015~2017年每年的资金投入按相同的增长率递增,求2015~2017年的年增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
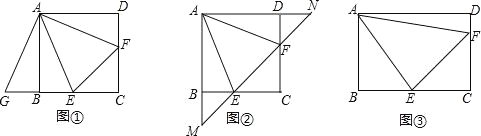
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com