
����Ŀ����ͼ����PΪ��ABC����ƽ����һ�㣬�ҡ�APB����BPC����CPA��120�������P������ABC�ķ����㣮
(1)�����PΪ��ǡ�ABC�ķ����㣬�ҡ�ABC��60��.
����֤�� ��ABP�ס�BCP��
����PA��3��PC��4����PB�ij���
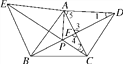
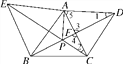
(2)��ͼ�ڣ���֪��ǡ�ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD�ཻ�ڵ�P������AP.
�����CPD�Ķ�����
����֤����PΪ��ABC�ķ����㣮

���𰸡���1�������� ��2��60�� ��3��������
(1)��֤�����ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60�������PAB����PBC.�֡ߡ�APB����BPC��120�������ABP�ס�BCP
�ڽ⣺�ɢٿ�֪��ABP�ס�BCP���� ![]() ����PB2��PA��PC��12����PB��2
����PB2��PA��PC��12����PB��2![]() .
.
(2)�ٽ⣺��ͼ���ߡ�ABE�͡�ACD���������Σ���AE��AB��AC��AD����EAB����5��60��.�ߡ�EAC����EAB����BAC����BAD����BAC����5�����EAC����BAD�����ACE�ա�ADB�����1����2.�ߡ�3����4�����CPD����5��60��.
��֤�����ɢٿ�֪��1����2����3����4�����ADF�ס�PCF����AF��PF��DF��CF����AF��DF��PF��CF.�ߡ�AFP����CFD�����AFP�ס�DFC�����APF����ACD��60��.�ɢٿ�֪��CPD��60�������APC����CPD����APF��120������BPC��180������CPD��120�������APB��360������BPC����APC��120�������PΪ��ABC�ķ����㣮
����������������� ![]() ���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�
���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�![]() ���������
���������![]() �ij�.
�ij�.![]() ��ͼ
��ͼ![]() ��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
���ɡ�CPD��60��.��֤����BPC��180������CPD��120����Ȼ��֤����ADF�ס�PCF�������������ε����ʺ��ж�������֤����AFP�ס�DFC���ʴ˿ɵõ���APF����ACD��60����Ȼ�����á�APC����CPD����APF��120��������������á�APB��360������BPC����APC��120��,����˵��.
���������
(1)�١ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60����
���PAB����PBC.�֡ߡ�APB����BPC��120����
���ABP�ס�BCP
���ɢٿ�֪��ABP�ס�BCP��
��![]()
��PB2��PA��PC��12��
![]()
(2)����ͼ���ߡ�ABE����ACD���������Σ�
��AE��AB��AC��AD����EAB����5��60��.
�ߡ�EAC����EAB����BAC����BAD����BAC����5��
���EAC����BAD��
���ACE�ա�ADB��
���1����2.
�ߡ�3����4��
���CPD����5��60��.
���ɢٿ�֪��1����2����3����4��
���ADF�ס�PCF��
��AF��PF��DF��CF��
��AF��DF��PF��CF.
�ߡ�AFP����CFD��
���AFP�ס�DFC��
���APF����ACD��60��.
�ɢٿ�֪��CPD��60����
���APC����CPD����APF��120����
��BPC��180������CPD��120����
���APB��360������BPC����APC��120����
���PΪ��ABC�ķ����㣮


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����зֽ���ʽ�Ĺ��̣�
x2+2ax��3a2
=x2+2ax+a2��a2��3a2���ȼ���a2���ټ�ȥa2��
=��x+a��2��4a2��������ȫƽ����ʽ��
=��x+a+2a����x+a��2a ��������ƽ���ʽ��
=��x+3a����x��a��
����������ͨ���Ӽ��������ȫƽ��ʽ���ٰѶ�������ʽ�ֽ���ʽ�ķ����������䷽����
�������䷽���ֽ���ʽ��m2��4mn+3n2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
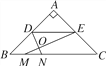
����Ŀ����ͼ����Rt��ABC�У���A��90�㣬AB��AC��BC��20��DE�ǡ�ABC����λ�ߣ���M�DZ�BC��һ�㣬BM��3����N���߶�MC�ϵ�һ�����㣬����DN��ME��DN��ME�ཻ�ڵ�O.����OMN��ֱ�������Σ���DO�ij���________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����У�ֱ���һ��һŮ��4����ʦ������ũ����ѧ֧�̣�
��1�����Ӽס�����У�����Ľ�ʦ�зֱ����ѡ1��������ѡ��2����ʦ�Ա���ͬ�ĸ����� ��
��2�����ӱ�����4����ʦ�����ѡ2�������б�����״ͼ�ķ��������2����ʦ����ͬһ��ѧУ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������У����ߺ������Խǵ����ҵı���ȣ���![]() �������������ۿ������������Ŀ���磺
�������������ۿ������������Ŀ���磺
��![]() �У�����A=45�㣬��B=30�㣬a=6����b��
�У�����A=45�㣬��B=30�㣬a=6����b��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com