【题目】观察下列分解因式的过程：
x2+2ax﹣3a2
=x2+2ax+a2﹣a2﹣3a2（先加上a2，再减去a2）
=（x+a）2﹣4a2（运用完全平方公式）
=（x+a+2a）（x+a﹣2a ）（运用平方差公式）
=（x+3a）（x﹣a）
像上面那样通过加减项配出完全平方式后再把二次三项式分解因式的方法，叫做配方法．
请你用配方法分解因式：m2﹣4mn+3n2
轻松夺冠全能掌控卷系列答案科目：初中数学 来源： 题型：
【题目】加、减、乘、除是我们常用的四种运算，它们分别用＋、－、×、÷来表示．现在我们来规定一种新的运算※，规定：a※b＝a2－ab，如果1※x＝1，求x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．
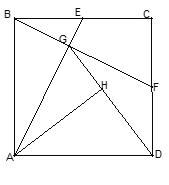
(1) 求证：△ABE≌△BCF；
(2) 若正方形边长为4，AH=
，求△AGD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】年初，工信部官网发布了2016年通信运营业统计公报，数据显示，2016年，4G用户数呈爆发式增长，全年新增3.4亿户，总数达到770 000 000亿户，将770 000 000用科学记数法表示应为（ ）
A.0.77×109
B.7.7×107
C.7.7×108
D.7.7×109
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是圆O的切线，切点为B，直线AO交圆O于C、D两点，CD＝2，∠DAB＝30°，动点P在直线AB上运动，PC交圆O于另一点Q.
(1)当点P运动到Q、C两点重合时(如图①)，求AP的长；
(2)点P运动过程中，有几个位置(几种情况)使△CQD的面积为
(直接写出答案)?
(3)当使△CQD的面积为，且Q位于以CD为直径的半圆上，CQ＞QD时(如图②)，求AP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
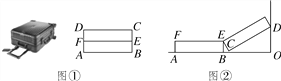
【题目】如图①所示的旅行箱的箱盖和箱底两部分的厚度相同，四边形ABCD为形如矩形的旅行箱一侧的示意图，F为AD的中点，EF∥CD.现将放置在地面上的箱子打开，使箱盖的一端点D靠在墙上，O为墙角，图②为箱子打开后的示意图．箱子厚度AD＝30cm，宽度AB＝50cm.
(1)图②中，EC＝________cm，当点D与点O重合时，AO的长为________cm；
(2)若∠CDO＝60°，求AO的长(结果取整数值，参考数据：sin60°≈0.87，cos60°＝0.5，tan60°≈1.73，可使用科学计算器)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，P为△ABC所在平面上一点，且∠APB＝∠BPC＝∠CPA＝120°，则点P叫作△ABC的费马点．
(1)如果点P为锐角△ABC的费马点，且∠ABC＝60°.
①求证： △ABP∽△BCP；
②若PA＝3，PC＝4，求PB的长；
(2)如图②，已知锐角△ABC，分别以AB，AC为边向外作正△ABE和正△ACD，CE和BD相交于点P，连接AP.
①求∠CPD的度数；
②求证：点P为△ABC的费马点．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
