【题目】已知AB是圆O的切线，切点为B，直线AO交圆O于C、D两点，CD＝2，∠DAB＝30°，动点P在直线AB上运动，PC交圆O于另一点Q.

(1)当点P运动到Q、C两点重合时(如图①)，求AP的长；

(2)点P运动过程中，有几个位置(几种情况)使△CQD的面积为(直接写出答案)?

(3)当使△CQD的面积为，且Q位于以CD为直径的半圆上，CQ＞QD时(如图②)，求AP的长．

参考答案：

【答案】（1）AP＝；（2）有4个位置；（3）AP＝.

【解析】试题分析：本小问是利用切线的性质，得到∠ACP＝90°，CD＝2，得到半径的长度：OD＝OC＝OB，从而利用解直角三角形的方法来解得AP的长度；利用三角形的面积公式，知底和积可求高，然后用平行线去截圆，即可以得到解；利用S△CQD＝，求出CD上的高QN的长度，过点PM⊥AD于点M，然后利用相似△QCN∽△DQN求出CN的长度，再次利用相似△PMC∽△QNC，从而得到MC与MP的关系，由已知易知AM＝，由AC＝1，从而可以解出MP，从而求出AP的长度.

试题解析：(1)、∵AB是圆O的切线 ∴∠OBA＝90°

∵ABC中，CD＝2，∠DAB=30° ∴OB＝1 ∴OB＝OC＝AC＝1

∵当点P，运动到Q、C两点重合时 ∴PC为圆O的切线 ∴∠PCA＝90°

∵∠DAB=30°，AC＝1 ∴AP＝

(2)、由于CD的长度2，而S△CQD＝，故CD上的高的长度为：，从而如图，我们可得到答案：

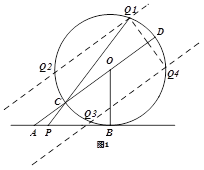
(3)、过点Q作QN⊥AD于点N， 过点P作PM⊥AD于点M ∵S△CQD＝

∴QN×CD＝∴CD＝∵CD是圆O的直径 ∴∠CQD＝90°

易证△QCN∽△DQN ∴∴

设CN＝X，则DN＝2－x ∴解得：

∵CQ＞QD ∴CN＝∴

易证：PMC∽△QNC 易得：∴

在AMP中易得：∵AM＋CM＝AC＝1

∴＋＝1 ∴MP＝∴AP＝2MP＝

关闭