
【题目】如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:AC=________,AB=________;
(2)判断△CAB和△DEF是否相似,并说明理由.

【答案】(1)2![]() 2
2![]() ;(2)相似,理由见解析
;(2)相似,理由见解析
【解析】试题分析: (1)根据勾股定理来求AC、AB的长度;
(2)由“三边法”法来证它们相似.
试题解析:
(1)如图,
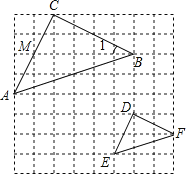
由勾股定理,得
AC=![]() =
=![]() .
.
AB=![]() =
=![]()
故答案是:![]() ,
,![]() ;
;
(2)△CAB和△DEF相似.理由如下:
如图,DE=DF=![]() =
=![]() ,EF=
,EF=![]() =
=![]() .
.
则![]() ,
,
所以△CAB∽△DEF.
点睛: 本题考查了相似三角形的判定,勾股定理,勾股定理的逆定理以及锐角三角函数的定义.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到Q、C两点重合时(如图①),求AP的长;
(2)点P运动过程中,有几个位置(几种情况)使△CQD的面积为![]() (直接写出答案)?
(直接写出答案)?
(3)当使△CQD的面积为![]() ,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.
,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
A.316×106
B.31.6×107
C.3.16×108
D.0.316×109
查看答案和解析>>
科目:初中数学 来源: 题型:
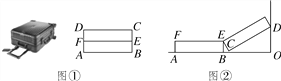
【题目】如图①所示的旅行箱的箱盖和箱底两部分的厚度相同,四边形ABCD为形如矩形的旅行箱一侧的示意图,F为AD的中点,EF∥CD.现将放置在地面上的箱子打开,使箱盖的一端点D靠在墙上,O为墙角,图②为箱子打开后的示意图.箱子厚度AD=30cm,宽度AB=50cm.
(1)图②中,EC=________cm,当点D与点O重合时,AO的长为________cm;
(2)若∠CDO=60°,求AO的长(结果取整数值,参考数据:sin60°≈0.87,cos60°=0.5,tan60°≈1.73,可使用科学计算器).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
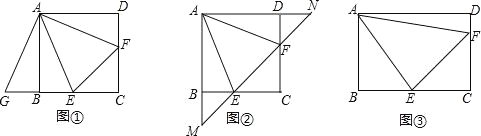
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查应作全面调查的是( )
A. 节能灯管厂要检测一批灯管的使用寿命.
B. 了解居民对废电池的处理情况.
C. 了解现代大学生的主要娱乐方式.
D. 某公司对退休职工进行健康检查.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com