练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，用长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，为了方便出入，在建造篱笆花圃时，在BC上用其他材料做了宽为1米的两扇小门．

    （1）设花圃的一边AB长为x米，请你用含x的代数式表示另一边AD的长为　 　米；

    （2）若此时花圃的面积刚好为45m2，求此时花圃的长与宽．

    【答案】（1）24﹣3x；（2）花圃的长为9米，宽为5米．

    【解析】（1）用绳子的总长减去三个AB的长，然后加上两个门的长即可表示出AD的长；

    （2）由在BC上用其他材料造了宽为1米的两个小门，故长边为22﹣3x+2，令面积为45，解得x．

    解：（1）设宽AB为x，

    则长AD=BC=22﹣3x+2=（24﹣3x）米；

    （2）由题意可得：（22﹣3x+2）x=45，

    解得：x1=3；x2=5，

    ∴当AB=3时，BC=15＞14，不符合题意舍去，

    当AB=5时，BC=9，满足题意．

    答：花圃的长为9米，宽为5米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若|a|=8，|b|=5，且a＞0，b＜0，a﹣b的值是（ ）
    A.3
    B.﹣3
    C.13
    D.﹣13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，点P、D分别是BC、AC边上的点，且∠APD＝∠B.

    (1)求证：AC·CD＝CP·BP；

    (2)若AB＝10，BC＝12，当PD∥AB时，求BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在由边长为1的小正方形组成的网格图中有△ABC，建立平面直角坐标系后，点O的坐标是（0，0）．

    （1）以O为位似中心，作△A′B′C′∽△ABC，相似比为1：2，且保证△A′B′C′在第三象限；

    （2）点B′的坐标为（_______），______）；

    （3）若线段BC上有一点D，它的坐标为（a，b），

    那么它的对应点D′的坐标为（__________）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．

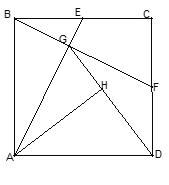
    (1) 求证：△ABE≌△BCF；

    (2) 若正方形边长为4，AH=，求△AGD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，四边形OABC是边长为4的正方形，M（4，m）、N（n，4）分别是AB、BC上的两个动点，且ON⊥MN，当OM最小时，＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=1，且经过点（3，0），则a﹣b+c的值为（ ）
    A.﹣1
    B.0
    C.1
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AB是圆O的切线，切点为B，直线AO交圆O于C、D两点，CD＝2，∠DAB＝30°，动点P在直线AB上运动，PC交圆O于另一点Q.

    (1)当点P运动到Q、C两点重合时(如图①)，求AP的长；

    (2)点P运动过程中，有几个位置(几种情况)使△CQD的面积为(直接写出答案)?

    (3)当使△CQD的面积为，且Q位于以CD为直径的半圆上，CQ＞QD时(如图②)，求AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．

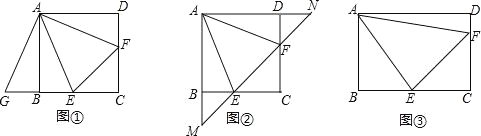
    （1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；

    （2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2；

    （3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．

    查看答案和解析>>

    同步练习册答案