
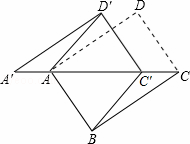
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(1)证明△A′AD′≌△CC′B;
(2)若∠ACB=30°,试问当点C'在线段AC上的什么位置时,四边形ABC′D′是菱形,并请说明理由.
科目:初中数学 来源: 题型:
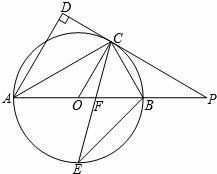
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若tan∠ABC=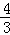 ,BE=7
,BE=7 ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.
(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A′C′的位置时,A′C′的长为 m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
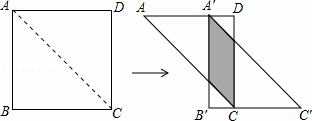
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知A(﹣3,1),B(﹣1,﹣1),C(﹣2,0),曲线ACB是以C为对称中心的中心对称图形,把此曲线沿x轴正方向平移,当点C运动到C′(2,0)时,曲线ACB描过的面积为 .
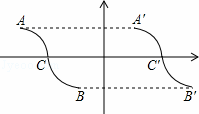
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一块矩形ABCD的场地,AB=102m,AD=51m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为( )

A. 5050m2 B.4900m2 C.5000m2 D. 4998m2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
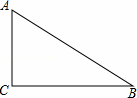
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com