下列几种形状的瓷砖中.只用一种不能够铺满地面的是( )A．正三角形B．正四边形C．正五边形D．正六边形题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

16．下列几种形状的瓷砖中，只用一种不能够铺满地面的是（　　）

A．

正三角形

B．

正四边形

C．

正五边形

D．

正六边形

分析根据平面图形镶嵌的条件：判断一种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角．若能构成360°，则说明能够进行平面镶嵌；反之则不能，对于一种正多边形的镶嵌应符合一个内角度数能整除360°，依此即可得出答案．

解答解：A、正三角形的每个内角是60°，能整除360°，能密铺；
B、正四边形的每个内角是90°，能整除360°，能密铺；
C、正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺；
D、正六边形的每个内角是120°，能整除360°，能密铺．
故选C．

点评此题考查了平面镶嵌，用到的知识点是只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

6．若4a²+12a+k是一个完全平方式，则k=9．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

7．在△ABC中，∠ABC=30°，∠BAC=70°．在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（　　）

A．

7条

B．

8条

C．

9条

D．

10条

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．下列运算正确的是（　　）

	A．	$\sqrt{（-11）^{2}}$=-11		B．	2$\sqrt{2}$-$\sqrt{2}$=1
	C．	（-$\sqrt{2}$）²=2		D．	$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

如图，在?ABCD中，对角线AC，BD交于点E，AC⊥BC，若BC=5，AB=13，则BD的长是2$\sqrt{61}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

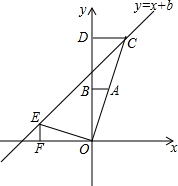如图，在平面直角坐标系中，点O是坐标原点，Rt△OAB的直角顶点B在y轴的正半轴上，以原点O为位似中心，位似比为2：1，把△OAB放大，放大后的三角形为△OCD，把△OAB绕点O逆时针旋转90°后得△OEF，点A的坐标是（1，t）．
（1）分别写出点C、E的坐标C（2，2t），E（-t，1）（用含t的代数式表示）；
（2）如果直线y=x+b经过E、C两点，试求出t与b的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

如图，一块含有60°三角板的顶点O在直线AB上，CD∥AB．则∠α=60度．