
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y=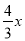 的图象交点为C(m,4)求:
的图象交点为C(m,4)求:
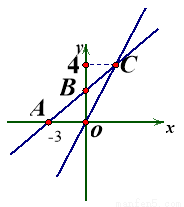
(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标。
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
(1) 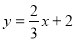 ;(2) (-2,5)或(-5,3).(3) (5,0)或(-5,0)或(6,0)或(
;(2) (-2,5)或(-5,3).(3) (5,0)或(-5,0)或(6,0)或(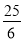 ,0).
,0).
【解析】
试题分析:(1)首先利用待定系数法把C(m,4)代入正比例函数y=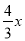 中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
(2)利用△BED1≌△AOB,△BED2≌△AOB,即可得出点D的坐标.
试题解析:(1)∵点C在正比例函数图像上 ∴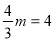 ,
,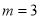
∵点C(3,4)A(—3,0)在一次函数图像上,
∴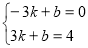
解这个方程组得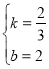
∴一次函数的解析式为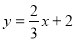
(2)过点D1作D1E⊥y轴于点E,过点D2作D2F⊥x轴于点F,
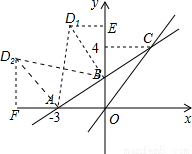
∵点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,∴AB=BD2,
∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°,∴∠BAO=∠EBD1,
∵在△BED1和△AOB中,

∴△BED1≌△AOB(AAS),
∴BE=AO=3,D1E=BO=2,
即可得出点D的坐标为(-2,5);
同理可得出:△AFD2≌△AOB,
∴FA=BO=2,D2F=AO=3,
∴点D的坐标为(-5,3).
综上所述:点D的坐标为(-2,5)或(-5,3).
(3)当OC是腰,O是顶角的顶点时,OP=OC=5,则P的坐标是(5,0)或(-5,0);
当OC是腰,C是顶角的顶点时,CP=CO,则P与O关于x=3对称,则P的坐标是(6,0).
当OC是底边时,设P的坐标是(a,0),则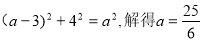
则P的坐标是:(5,0)或(-5,0)或(6,0)或(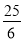 ,0).
,0).
考点:两条直线相交或平行问题.


科目:初中数学 来源:2014-2015学年四川省广安市白庙督导区七年级10月月考数学试卷(解析版) 题型:计算题
计算: (1)-∣-3∣×1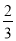 -
-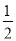 ÷(-6)
÷(-6)
﹙2)25×﹙-0.125﹚×﹙-4﹚×﹙-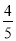 ) ×﹙-8﹚×1
) ×﹙-8﹚×1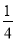
(3)1-2-3+4+5-6-7+8+…-2007+2008+2009-2010
(4)(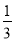 -
-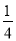 -
-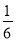 )×(-48)
)×(-48)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省片区七年级上学期期中联考数学试卷(解析版) 题型:选择题
在-(-4),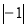 ,
,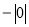 ,(-2)3这四个数中非负数共有( )个
,(-2)3这四个数中非负数共有( )个
A.1 B.4 C.2 D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都十校七年级12月联谊月考数学试卷(解析版) 题型:选择题
如图,数轴上A、B两点分别对应实数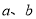 ,则下列结论正确的是( )
,则下列结论正确的是( )
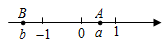
A.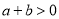 B.
B.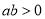 C.
C.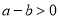 D.
D.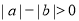
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片八年级12月月考数学试卷(解析版) 题型:解答题
有两棵树,一棵高7米,另一棵高2米,两树相距12米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,请问小鸟至少飞行多少米.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片八年级12月月考数学试卷(解析版) 题型:填空题
已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=____,b=_____;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市八年级上学期学情调研数学试卷(解析版) 题型:解答题
如图,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法:
①a为任意有理数, 总是正数;
总是正数;
②方程x+2= 是一元一次方程;
是一元一次方程;
③若 ,
, ,则
,则 ,
, ;
;
④ 代数式
代数式 、
、 、
、 都是整式 ;
都是整式 ;
⑤若a2=(-2)2, 则a=-2.其中错误的有
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com