
分析 根据定义和素数p,q满足f(p)=f(q)+242,可得(p-q)(p+q+1)=242,再将242分解成2×121和11×22,即可得出关于p、q的二元一次方程组,解方程组即可得出结论.
解答 解:∵定义f(x)=x2+x+1,素数p,q满足f(p)=f(q)+242,
∴p2+p+1=q2+q+1+242,即(p-q)(p+q+1)=242.
∵242=2×121=11×22,p、q为素数,
∴p-q<p+q+1,
∴$\left\{\begin{array}{l}{p-q=2}\\{p+q+1=121}\end{array}\right.$或$\left\{\begin{array}{l}{p-q=11}\\{p+q+1=22}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{p=61}\\{q=59}\end{array}\right.$或$\left\{\begin{array}{l}{p=16}\\{q=5}\end{array}\right.$,
∵p、q均为素数,
∴有序数对(p,q)=(61,59).
故答案为:(61,59).
点评 本题考查了质数与合数以及解二元一次方程组,解题的关键是通过拆分242得出关于p、q的二元一次方程组.本题属于中档题,难度不大,解决该题型题目时,通过分解合数得出方程(或方程组)是关键.


科目:初中数学 来源: 题型:选择题
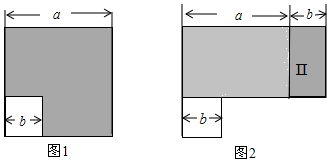
| A. | 60 | B. | 100 | C. | 125 | D. | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠BAD=∠ADC=90°.AB=AD=4,CD=3,点P在四边形ABCD的边长,若点P到BD的距离为$\sqrt{3}$,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°.AB=AD=4,CD=3,点P在四边形ABCD的边长,若点P到BD的距离为$\sqrt{3}$,则点P的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知Rt△ABC中,∠ABC=90°,BC=9,cosC=$\frac{3}{5}$,D是边AC上的动点,连接BD,过点D作ED⊥BD,交射线BA于点E,当△AED是等腰三角形时,CD的值为3或$\frac{54}{5}$.
如图,已知Rt△ABC中,∠ABC=90°,BC=9,cosC=$\frac{3}{5}$,D是边AC上的动点,连接BD,过点D作ED⊥BD,交射线BA于点E,当△AED是等腰三角形时,CD的值为3或$\frac{54}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校将一块三角形废地ABC,设计为一个花园,测得AC=80m,BC=60m,AB=100m.
如图,某校将一块三角形废地ABC,设计为一个花园,测得AC=80m,BC=60m,AB=100m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 通过计算图形的面积,可以获得一些有趣的发现.
通过计算图形的面积,可以获得一些有趣的发现.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com