
�о�����:һ�������ĺ���װ�����ɸ�ֻ����ɫ��һ���ĺ��������.�������㲻ͬ��ɫ�������?
��������:�ȴӺ�������8����,���ϼǺŷŻغ���,�ٽ�����������.���������Ҫ��:�Ƚ������,ÿ���������һ����,�Żغ���,�ټ���.
����:��������һ������50��,ͳ�ƽ�����±�:
�����ɫ | �Ǻ� | �мǺ� | ||
��ɫ | ��ɫ | ��ɫ | ��ɫ | |
�����Ĵ��� | 18 | 28 | 2 | 2 |
�Ʋ����.���������������������:
(1)���к������ռ�������İٷֱ��Ƕ���?
(2)�����к�����ٸ�?

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ������������2018-2019ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ����Rt��ABC������ƽ��ֱ������ϵ�У�C��ԭ���غϣ�CB��x���ϣ���AB=2����B������Ϊ��4��0�������A������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ���2018����꼶�ϲ������ۺϼ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ��һ���鱾��ֽ������ԭֽ�Ŷ�ζԿ��õ���.����



 ���ڣ� ��.
���ڣ� ��.

A. 
 C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶��ѧ�ϲ����и�ϰ�ۺϼ���Ծ���1-4�£� ���ͣ������
��ͼ���ڱ߳�Ϊ









�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶��ѧ�ϲ����и�ϰ�ۺϼ���Ծ���1-4�£� ���ͣ���ѡ��
����
 ��ʵ��������
��ʵ��������
A.  B.
B.  ��
��
 D.
D.  ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ�ϲ��ۺϼ���Ծ� ���ͣ������
��֪���κ��� ��
��













�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ����Rt��ABC�У���ABC��90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC���е㣬����DE.
(1)��֤��DE�ǡ�O�����ߣ�
(2)����BAC��30�㣬DE��3����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
һԪ���η���x2��2x�Ľ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п�ģ���Ծ� ���ͣ������
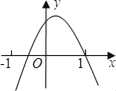
��ͼ��������y=ax2+bx+c��a��0���������£���x����������ڵ㣨1��0���������н��ۣ���abc��0����a��b+c��0����2a+b��0����a+b+c=1��������ȷ����_____ ������ţ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com