
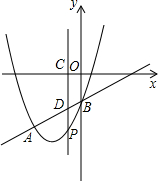
 如图,抛物线y=x2+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
如图,抛物线y=x2+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
|

|
| -m(1+1-m) |
| 2 |
| -m(-3m-m2) |
| 2 |
| 1 |
| 2 |
| -m(1+1-m) |
| 2 |
| -m(2-5m-m2) |
| 2 |
-7+
| ||
| 4 |
-7-
| ||
| 4 |
| 1 |
| 2 |
-7-
| ||
| 4 |
| 2 |

| AP |
| CF |
| DP |
| CD |
| m+3 |
| 1-m |
| -3m-m2 |
| 1-m |
| 2 |
| 4 |
| -3-m |
4
| ||
| AD |
| 2 |
| PD |
| FA |
| AD |
| AE |
| 3m+m2 | ||
4
|
| ||
| 4 |


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
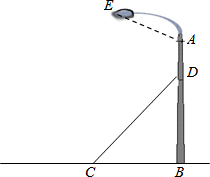 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且CB=5米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且CB=5米.查看答案和解析>>
科目:初中数学 来源: 题型:
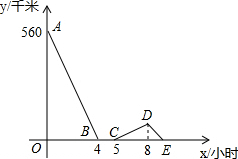 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
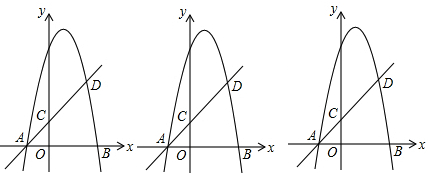
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com