
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

【答案】(1)证明见解析;(2)∠AED+∠D=180°,理由见解析;(3)110°
【解析】
(1)依据同位角相等,即可得到两直线平行;
(2)依据平行线的性质,可得出∠FGD=∠EFG,进而判定AB∥CD,即可得出∠AED+∠D=180°;
(3)依据已知条件求得∠CGF的度数,进而利用平行线的性质得出∠CEF的度数,依据对顶角相等即可得到∠AEM的度数.
(1)∵∠CED=∠GHD,
∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布的扇形统计图,其中八年级人数为408人,下表是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人阅读课外书________本.
图书种类 | 频数 | 频率 |
科普知识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛记 | A | 0.25 |
其他 | 144 | 0.06 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC 平分∠BAD,过 C 点作 CE⊥AB 于 E,并且 2AE=AB+AD,则下列结论:
①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE,其中不正确的结论个数有( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
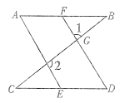
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com