
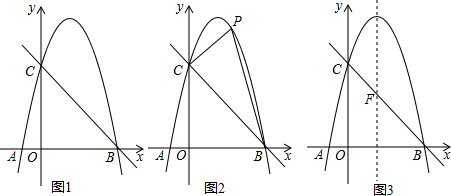
���� ��1������������y=ax2+bx-4a����A��-1��0����C��0��4�����㣬�г�a��b�Ķ�Ԫһ�η����飬���a��b��ֵ�����������B�����꣬�������ֱ��BC�Ľ���ʽ��
��2������P��PQ��y�ᣬ��ֱ��BC��Q����P��x��-x2+3x+4������Q��x��-x+4�������PQ�ij�������S��PCB=$\frac{1}{2}$PQ•OB�г�S����x�Ķ��κ��������ú��������������������ֵ�����������P�����ꣻ
��3���������EF�ij�����N��x��-x2+3x+4������M��x��-x+4��������ƽ���ı��ζԱ�ƽ��������г�x��һԪ���η��̣��ⷽ�����x��ֵ���ɣ�
��� �⣺��1�������⣬�У�$\left\{\begin{array}{l}a-b-4a=0\\-4a=4\end{array}\right.$��
���$\left\{\begin{array}{l}a=-1\\ b=3\end{array}\right.$��
�������ߵĽ���ʽ��y=-x2+3x+4��
����B��4��0����C��0��4����֪��ֱ��BC��y=-x+4��
��2����B��4��0����C��0��4����֪��ֱ��BC��y=-x+4��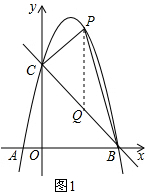
��ͼ1������P��PQ��y�ᣬ��ֱ��BC��Q����P��x��-x2+3x+4������Q��x��-x+4����
��PQ=��-x2+3x+4��-��-x+4��=-x2+4x��
S��PCB=$\frac{1}{2}$PQ•OB=$\frac{1}{2}$����-x2+4x����4=-2��x-2��2+8��
�൱P��2��6��ʱ����PCB��������
��3�����ڣ�
������y=-x2+3x+4�Ķ�������E��$\frac{3}{2}$��$\frac{25}{4}$����
ֱ��BC��y=-x+4����x=$\frac{3}{2}$ʱ�� F��$\frac{3}{2}$��$\frac{5}{2}$����
F��$\frac{3}{2}$��$\frac{5}{2}$����
��EF=$\frac{15}{4}$��
��ͼ2������M��MN��EF����ֱ��BC��M����N��x��-x2+3x+4������M��x��-x+4����
��MN=|��-x2+3x+4��-��-x+4��|=|-x2+4x|��
��EF��NMƽ�������ʱ���ı���EFMN��ƽ���ı��Σ�
��|-x2+4x|=$\frac{15}{4}$��
��-x2+4x=$\frac{15}{4}$ʱ�����x1=$\frac{5}{2}$��x2=$\frac{3}{2}$���������⣬��ȥ����
��x=$\frac{5}{2}$ʱ��y=-��$\frac{5}{2}$��2+3��$\frac{5}{2}$+4=$\frac{21}{4}$��
��N1��$\frac{5}{2}$��$\frac{21}{4}$����
��-x2+4x=-$\frac{15}{4}$ʱ�����x=$\frac{4��\sqrt{31}}{2}$��
��x=$\frac{4+\sqrt{31}}{2}$ʱ��y=$\frac{-7-2\sqrt{31}}{4}$��
��N2��$\frac{4+\sqrt{31}}{2}$��$\frac{-7-\sqrt{31}}{4}$����
��x=$\frac{4-\sqrt{31}}{2}$ʱ��y=$\frac{-7+2\sqrt{31}}{4}$��
��N3��$\frac{4-\sqrt{31}}{2}$��$\frac{-7+2\sqrt{31}}{4}$����
������������N������$\frac{5}{2}$��$\frac{21}{4}$������$\frac{4+\sqrt{31}}{2}$��$\frac{-7-\sqrt{31}}{4}$������$\frac{4-\sqrt{31}}{2}$��$\frac{-7+2\sqrt{31}}{4}$����
���� ������Ҫ�����˶��κ����ۺ��⣬�����漰������ϵ������������ʽ�����κ��������ʡ�����������ļ��㡢ƽ���ı��ε��ж���֪ʶ�����2���ʹؼ�����x��ʾ��PQ�ij������3���ʹؼ������EF�ij�������ƽ���ı��ζԱ�ƽ������Ƚ��н�𣬴�����һ�����Ѷȣ�


 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
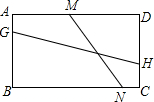 ��ͼ����֪����ABCD��AD=9��AB=6������G��H��M��N�ֱ���AB��CD��AD��BC�ϣ��߶�MN��GH���ڵ�K������GKM=45�㣬NM=3$\sqrt{5}$����GH=3$\sqrt{10}$��
��ͼ����֪����ABCD��AD=9��AB=6������G��H��M��N�ֱ���AB��CD��AD��BC�ϣ��߶�MN��GH���ڵ�K������GKM=45�㣬NM=3$\sqrt{5}$����GH=3$\sqrt{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | һ | �� | �� | �� | �� | �� | �� |
| ���� | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
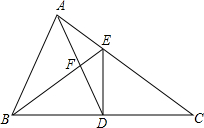 ��ͼ����ABC�У�D��E�ֱ�ΪBC��AC��һ�㣬AB=AD��BE=EC��
��ͼ����ABC�У�D��E�ֱ�ΪBC��AC��һ�㣬AB=AD��BE=EC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
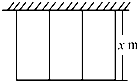 ��ͼ��ʾ��һ��ũ����24m�������Χ��һ��һ�濿ǽ����С����ұ˴��������������μ��ᣬҪʹ��������������Ϊ36m2�������ÿ������ij�Ϊx m�����������г��ķ����ǣ�24-4x��•x=36��
��ͼ��ʾ��һ��ũ����24m�������Χ��һ��һ�濿ǽ����С����ұ˴��������������μ��ᣬҪʹ��������������Ϊ36m2�������ÿ������ij�Ϊx m�����������г��ķ����ǣ�24-4x��•x=36���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -x2y��x2y2 | B�� | x2y2��2xy | C�� | -x2y��3x2y | D�� | xy2��x2y |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com