解:(1)∵∠OAB=30°,AB=4

,
∴OB=

AB=

×4

=2

,
∵S
△AOB=

OB•OA=

×2

•OA=6

,
∴OA=6,
∴点A、B的坐标为A(0,6),B(2

,0);
(2)①当点P为线段OA的中点时,直线BP将△AOB分成面积相等的两部分,

∴点P的坐标为(0,3),
设直线BP的解析式为y=kx+b,
则
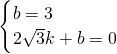
,
解得
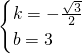
,
∴直线BP的解析式为y=-

x+3;
②当E为线段AB的中点时,PE与PB的和最小.
理由如下:
作△AOB关于y轴的对称图形△AOC,
∵∠OAB=30°,
∴△ABC是等边三角形,
过点B作BF⊥AC交OA于点P,过点P作PE⊥AB,根据轴对称性可知PE=PF,根据垂线段最短可知点P为所求作的点,
根据等边三角形的性质,PA=PB,∠PBO=30°,
∴∠ABP=60°-30°=30°,
∴∠ABP=∠BAO=30°,
∴AP=BP,
在Rt△PBO中,∠PBO=30°,
∴PB=2PO,
∴OA=OP+AP=OP+2OP=6,
解得OP=2,
∴点P的坐标为(0,2).
分析:(1)根据直角三角形30°角所对的直角边等于斜边的一半求出OB的长度,再利用三角形的面积公式求出AO的长度,从而得解;
(2)①根据三角形的面积公式求出OP的长,求出点P的坐标,再利用待定系数法列式求解即可;
②作△AOB关于y轴的对称图形△AOC,可得△ABC是等边三角形,作BF⊥AC,根据垂线段最短可得BF与y轴的交点就是所要求作的点P,求出∠BAP=∠ABP=30°,根据等角对等边可得AP=BP,再根据直角三角形30°角所对的直角边等于斜边的一半可得BP=2OP,然后代入数据求出OP的长度,从而求出点P的坐标.
点评:本题综合考查了一次函数的问题,待定系数法求直线的解析式,直角三角形30°角所对的直角边等于斜边的一半的性质,等边三角形的性质,以及轴对称的性质,综合性较强,作轴对称图形,找出点P的位置然后再进行说明求解.

 ,S△AOB=6
,S△AOB=6 .
.
 ,
, AB=
AB= ×4
×4 =2
=2 ,
, OB•OA=
OB•OA= ×2
×2 •OA=6
•OA=6 ,
, ,0);
,0);
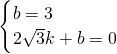 ,
,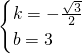 ,
, x+3;
x+3;

 阅读快车系列答案
阅读快车系列答案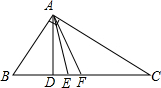 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=