△ABC和△A1B1C1满足下列条件:
①∠A=68°,∠B=40°,∠A1=68°,∠C1=72°;
②∠A=120°,AB=7,AC=14,∠A1=120°,A1B1=3,A1C1=6;
③AB=4,BC=6,AC=7,A1B1=12,B1C1=18,A1C1=21;
④AB=2,BC=3,∠A=61°,A1B1=4,B1C1=6,∠A=61°.
其中能判定△ABC和△A1B1C1相似的有________.
①②③
分析:根据相似三角形的判定定理进行判断.
解答:①根据三角形内角和定理得到∠C=72°,则在△ABC和△A
1B
1C
1中,∠A=∠A
1=68°,∠C=∠C
1=72°,所以△ABC和△A
1B
1C
1相似.故①正确;
②根据题意知∠A=120°,∠A
1=120°,
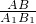
=
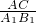
=

,所以△ABC和△A
1B
1C
1相似.故②正确;
③根据题意知:AB:A
1B
1=BC:B
1C
1=AC:A
1C
1=1:3.所以△ABC和△A
1B
1C
1相似.故③正确;
④若∠B=∠B
1时,△ABC和△A
1B
1C
1才相似.故④不一定正确;
综上所述,能判定△ABC和△A
1B
1C
1相似的有①②③.
故答案是:①②③.
点评:本题考查了相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角.

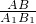 =
=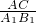 =
= ,所以△ABC和△A1B1C1相似.故②正确;
,所以△ABC和△A1B1C1相似.故②正确;

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案