
| 册数 | 4 | 5 | 6 | 7 | 8 | 50 |
| 人数 | 6 | 8 | 15 | 2 |
分析 (1)根据:全班40名同学和共捐图书320册这两个相等关系,设捐献7册的人数为x,捐献8册的人数为y,就可以列出方程组解决.
(2)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.平均数是指在一组数据中所有数据之和再除以数据的个数.然后根据它们的意义判断.
解答  解:(1)设捐献7册的人数为x,捐献8册的人数为y,则
解:(1)设捐献7册的人数为x,捐献8册的人数为y,则
$\left\{\begin{array}{l}{x+y=40-6-8-15-2=9}\\{7x+8y=320-(4×6+5×8+6×15+50×2)=66}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$
答:捐献7册的人数为6人,捐献8册的人数为3人;
(2)捐书册数的平均数为320÷40=8,
按从小到大的顺序排列得到第20,21个数均为6,所以中位数为6,
出现次数最多的是6,所以众数为6,
因为平均数8受两个50的影响较大,所以平均数不能反映该班同学捐书册数的一般情况.
点评 此题考查了众数、中位数及加权平均数的知识,解题关键是要读懂题目的意思,找出合适的等量关系:即班级捐献7册图书人数+捐献8册图书的人数=总人数-捐献4册图书人数-捐献5册图书人数-捐献6册图书人数-捐献50册图书人数,捐献7册图书的总册数+捐献8册图书的总册数=总册数-捐献4册图书的总册数-捐献5册图书的总册数-捐献6册图书的总册数-捐献50册图书的总册数,列出方程组,再求解.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:选择题
| A. | 32 | B. | 36 | C. | 40 | D. | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
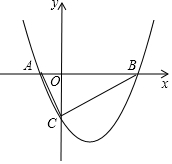 抛物线y=ax2+bx-2与x轴交于点A(-1,0),B(m,0)两点,与y交于点C,且∠ACB=90°,则该抛物线的解析式为y=0.5x2-1.5x-2.
抛物线y=ax2+bx-2与x轴交于点A(-1,0),B(m,0)两点,与y交于点C,且∠ACB=90°,则该抛物线的解析式为y=0.5x2-1.5x-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 素质测试 | 测试成绩 | |||
| 李兵 | 张军 | 赵海 | 王洋 | |
| 计算机 | 70 | 80 | 75 | 70 |
| 商品知识 | 60 | 65 | 75 | 65 |
| 语言 | 80 | 75 | 70 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
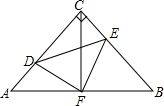 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF.
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
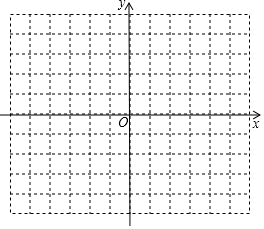 如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).
如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -52 与(-5)2相等 | |
| B. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| C. | -a2表示一个负数 | |
| D. | 两个有理数的差不一定小于被减数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com