
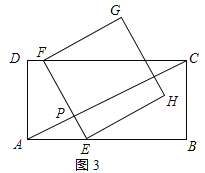
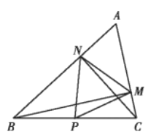
����Ŀ����ͼ���ھ���![]() �У�
��![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��4����λ���ȵ��ٶ����յ�
��ÿ��4����λ���ȵ��ٶ����յ�![]() �˶�.����
�˶�.����![]() �������
�������![]() ��
��![]() �غϣ���
�غϣ���![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��������������
��������������![]() .���
.���![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��.
��.
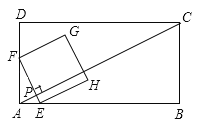
��1����![]() _________________��
_________________��
�ڵ���![]() ��
��![]() ��ʱ���ú�
��ʱ���ú�![]() �Ĵ���ʽֱ�ӱ�ʾ�߶�
�Ĵ���ʽֱ�ӱ�ʾ�߶�![]() �ij�.
�ij�.
��2������![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() ��ֵ��
��ֵ��
��3����������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4��ֱ��д���Խ���![]() ���ڵ�ֱ�߽�������
���ڵ�ֱ�߽�������![]() �ֳ�������ͼ�ε������Ϊ1��2ʱ
�ֳ�������ͼ�ε������Ϊ1��2ʱ![]() ��ֵ.
��ֵ.
���𰸡���1����15����![]() ����2��t��
����2��t��![]() ����3��
����3��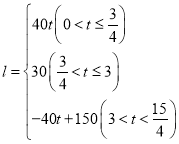 ����4��
����4��![]() ��
��![]() .
.
��������
��1�����ɾ��ε����ʺ��ɶ������ɵó������
����֤����APF�ס�ADC���ɵ�![]() ����һ�����ɵó������
����һ�����ɵó������
��2������F���D�غ�ʱ����ͼ1��֤����APD�ס�ADC���ó�![]() ����һ��������ý����
����һ��������ý����
��3����������ۣ�
����0��t��![]() ʱ����ͼ2��ʾ���ɣ�1�����ã�PF��8t��ͬ���ɵã�PE��t�Ĺ�ϵ���Ӷ��ɵ�EF��t�Ĺ�ϵ�������ɵý����
ʱ����ͼ2��ʾ���ɣ�1�����ã�PF��8t��ͬ���ɵã�PE��t�Ĺ�ϵ���Ӷ��ɵ�EF��t�Ĺ�ϵ�������ɵý����
����![]() ��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ������ʱEF�ij����ɵó������
��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ������ʱEF�ij����ɵó������
����3��t��![]() ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��Ȼ���������������ε����ʼ��ɵó�PF��PE��t�Ĺ�ϵ�������ɵ�EF��t�Ĺ�ϵʽ�����⼴�ý����
ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��Ȼ���������������ε����ʼ��ɵó�PF��PE��t�Ĺ�ϵ�������ɵ�EF��t�Ĺ�ϵʽ�����⼴�ý����
��4���ɣ�2�����֪���Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱ��ֻ����ͼ3�п��ܳ��֣��ٷ�PE��PF��1��2��PF��PE��1��2����������������������ε����ʺ�ͼ3�Ľ��ۣ�EF=10������⼴�ɣ�
�⣺��1�������ı���ABCD�Ǿ��Σ����B��90�㣬
��AC��![]() ��
��
�ʴ�Ϊ��15��
�����ı���ABCD�Ǿ��Σ����D��90�㣬AD��BC��3![]() ��CD��AB��6
��CD��AB��6![]() ��
��
��EF��AC�����APF��90�㣽��D��
�ߡ�PAF����DAC�����APF�ס�ADC��
��![]() ����
����![]() ����ã�PF��8t��
����ã�PF��8t��
��2������F���D�غ�ʱ����ͼ1��ʾ��
�ߡ�APD����ADC��90�㣬��PAD����DAC��
���APD�ס�ADC��
��![]() ����
����![]() ��
��
��ã�t��![]() ��
��
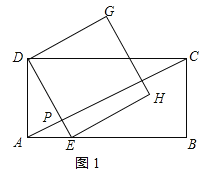
��3������0��t��![]() ʱ����ͼ2��ʾ��
ʱ����ͼ2��ʾ��
�ɣ�1�����ã�PF��8t��ͬ������ã�PE��2t����EF��10t��
��l��4EF��40t��
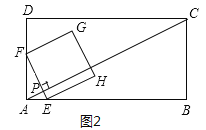
����![]() ��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ�
��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ�
��EF��10t��![]() ����l��4��
����l��4��![]() ��30��
��30��
����3��t��![]() ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��
ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�PF��![]() ��15��4t����PE��2��15��4t����
��15��4t����PE��2��15��4t����
��EF��PF+PE��![]() ��15��4t����
��15��4t����
��l��4��![]() ��15��4t������40t+150��
��15��4t������40t+150��
���ϣ�![]() ��
��![]() ֮��ĺ�����ϵʽ�ǣ�
֮��ĺ�����ϵʽ�ǣ�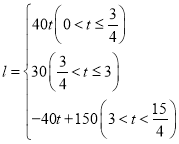 ��
��
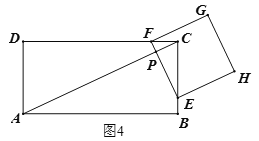
��4���ɣ�2�����֪���Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱ��ֻ����ͼ3�п��ܳ��֣���PE��PF��1��2����PF��PE��1��2��
��PE��PF��1��2ʱ����EF��![]() ����PF��
����PF��![]() EF��5��
EF��5��
�ߡ�CPF�ס�CDA����![]() ����
����![]() ����ã�PF��
����ã�PF��![]() ��15��4t����
��15��4t����
��![]() ��15��4t����5����ã�t��
��15��4t����5����ã�t��![]() ��
��

��PF��PE��1��2ʱ��PF��![]() EF��
EF��![]() ����
����![]() ��15��4t����
��15��4t����![]() ����ã�t��
����ã�t��![]() ��
��
�����������Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱt��ֵΪ![]() ��
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
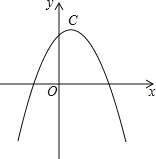
����Ŀ����ͼ��������![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ���������ߵĶԳ���Գƣ�����
���������ߵĶԳ���Գƣ�����![]() ��
��![]() �ᣬ��
�ᣬ��![]() ���ڵ�
���ڵ�![]() .
.
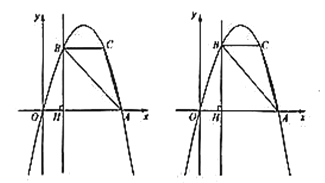
��1���������ߵĽ���ʽ��
��2��ֱ��д��![]() �����꣬����
�����꣬����![]() �������
�������
��3����![]() Ϊ��������һ���㣬��λ�ڵ������ޣ���
Ϊ��������һ���㣬��λ�ڵ������ޣ���![]() ���Ϊ6ʱ�����
���Ϊ6ʱ�����![]() �����ꣻ
�����ꣻ
��4������![]() ��ֱ��
��ֱ��![]() ���˶�����
���˶�����![]() ��
��![]() �����˶�������
�����˶�������![]() ��
��![]() ��
��![]() Ϊ�����������Ϊ����ֱ��������ʱ��ֱ��д����ʱ��
Ϊ�����������Ϊ����ֱ��������ʱ��ֱ��д����ʱ��![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
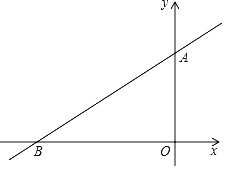
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() �ߵ��е㣬����
�ߵ��е㣬����![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
����![]() Ϊ�ȱ������Σ��ܵ�
Ϊ�ȱ������Σ��ܵ�![]() ʱ��
ʱ��![]() .�뽫��ȷ���۵�������ں�����__.
.�뽫��ȷ���۵�������ں�����__.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ڣ���������ͬһֱ���ϵĵ�A��B��C����ͼ��ʾ����O����A��B��C�ľ��������a��aΪ������������O�ľ������a�����е����ͼ��G��![]() ��ƽ���߽�ͼ��G�ڵ�D������AD��CD��
��ƽ���߽�ͼ��G�ڵ�D������AD��CD��
��1����֤��AD=CD��
��2������D��DE![]() BA������ΪE����DF
BA������ΪE����DF![]() BC������ΪF���ӳ�DF��ͼ��G�ڵ�M������CM����AD=CM����ֱ��DE��ͼ��G�Ĺ����������
BC������ΪF���ӳ�DF��ͼ��G�ڵ�M������CM����AD=CM����ֱ��DE��ͼ��G�Ĺ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������C1��y1=��2x2+4x+2��C2��y2=��x2+mx+n�Ķ�����ͬ����
��1����������C2�Ľ���ʽ.
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ᡢy��ֱ��ཻ�ڵ�A��B����C������OA�ϣ���D������OB�ϣ���OD��2OC����CD���е�Ϊ�Գ���������COD�ĶԳ�ͼ�Ρ�DEC�����C������Ϊ��0��n������DEC��ֱ��AB�·����ֵ����ΪS��
��x�ᡢy��ֱ��ཻ�ڵ�A��B����C������OA�ϣ���D������OB�ϣ���OD��2OC����CD���е�Ϊ�Գ���������COD�ĶԳ�ͼ�Ρ�DEC�����C������Ϊ��0��n������DEC��ֱ��AB�·����ֵ����ΪS��
��1������E��AB��ʱ��n���� ��������D���B�غ�ʱ��n���� ����
��2����S����n�ĺ�������ʽ����ֱ��д���Ա���n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������������취��������������������86�γ����������ͨ������2019��9��l����ʩ��.Ϊ�˽�ͬѧ�Ƕ�����������֪ʶ�����˽�������ź����ھ��꼶�����ȡ��������ͬѧ�������ʾ����飬����������Ϊ�����ĸ��ȼ���![]() ���dz��˽⡢
���dz��˽⡢![]() ���Ƚ��˽⡢
���Ƚ��˽⡢![]() ��֪���ĺ��١�
��֪���ĺ��١�![]() ����ȫ���˽�.�������������Ƴ�����������������ͳ��ͼ.
����ȫ���˽�.�������������Ƴ�����������������ͳ��ͼ.
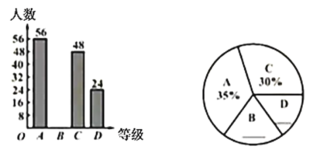
��1����ȫ���������ͳ��ͼ������ͳ��ͼ��
��2������ȡͬѧ�ʾ��������λ�������ĸ��ȼ�___________������ĸ����
��3�������꼶��1300��ͬѧ���꼶�����Ե�����Ϊ��֪���ĺ�����������ȫ���˽�����������ͬѧ����������������֪ʶ���ռ�����ѵ�����������꼶�ж�������Ҫ����������������֪ʶ���ռ�����ѵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������̶��ڼס����������������۵�ij��Ʒ�����о��������¹���:ÿ�������Ϊ![]() (��)ʱ�����ȫ������
(��)ʱ�����ȫ������![]() (��Ԫ)��
(��Ԫ)��![]() �����ϵʽ
�����ϵʽ![]() ,Ͷ���г�������ȫ����10�������ڼס�������ÿ�ֵ��ۼ�
,Ͷ���г�������ȫ����10�������ڼס�������ÿ�ֵ��ۼ�![]() (��Ԫ)����
(��Ԫ)����![]() ����һ�κ�����ϵ.(ע:������=�����۶�-ȫ������)
����һ�κ�����ϵ.(ע:������=�����۶�-ȫ������)
(1)���ڼ�����������![]() ��ʱ,����
��ʱ,����![]() �����ڼ����ɲ�����
�����ڼ����ɲ�����![]() ��ʱ����Ϊ������Ԫ��
��ʱ����Ϊ������Ԫ��
(2)�����ҵ�����������![]() ��ʱ,
��ʱ,![]() ,�����ҵص�������������ӦΪ������Ԫ?
,�����ҵص�������������ӦΪ������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
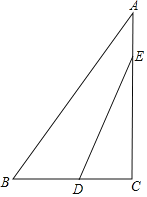
����Ŀ����ͼ����Rt��ABC�У���ACB��90����AC��8��BC��6.��E�ӵ�A��������AC��ÿ��1����λ���ȵ��ٶ����յ�C�˶�����D�ӵ�C��������CһBһA��ÿ��2����λ���ȵ��ٶ����յ�A�˶�������Eֹͣ�˶�ʱ����D��ֹ֮ͣ����E��Dͬʱ���������E���˶�ʱ��Ϊt(��)
(1)�ú�t�Ĵ���ʽ��ʾCE�ij���
(2)���D��CA�ľ���Ϊh���ú�t�Ĵ���ʽ��ʾh��
(3)���CDE�����ΪS(ƽ����λ)����S(ƽ����λ)��t(��)�ĺ�����ϵʽ��
(4)��DE���ABC�ı�ƽ�л�ֱʱ��ֱ��д��t��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com