
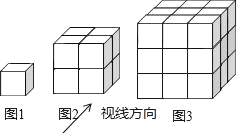
【题目】如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A. 271 B. 272 C. 331 D. 332
【答案】C
【解析】
根据图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
归纳出变化规律:
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,将第11个代入即可求解.
图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,
所以则第11个图形中,其中看得见的小立方体有113-103=331个,
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
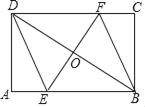
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )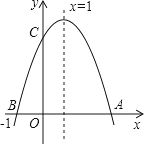
A.①④
B.①③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆放假时,小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆。早上从家里出发,向东走了6千米到超市买东西,然后又向东走了1.5千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里。
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家所经历路程小车的耗油量。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。

⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月29日,国家发改委批复了昌景黄铁路项目可行性研究报告.该项目位于赣皖两省,线路起自江西省南昌市南昌东站,经上饶市、景德镇市,安徽省黄山市,终至黄山北站.按照设计,行驶180千米,昌景黄高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少20分钟,求昌景黄高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com