
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
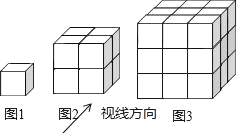
A. 271 B. 272 C. 331 D. 332
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
四川的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区。已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点。从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元。设从B地运往C处的蔬菜为![]() 吨。
吨。
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时![]() 的值?
的值?
C | D | 总计 | |
A | 200吨 | ||
B |
| 300吨 | |
总计 | 240吨 | 260吨 | 500吨 |
(2)已知总运费最小的调运费用是9280元,请你提交具体的调运方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
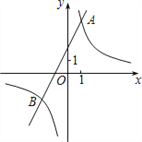
【题目】如图,已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=﹣3时,求二次函数图象的顶点坐标;
(2)当c=10时,若在函数值y=1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(3)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).
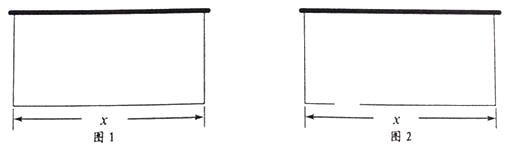
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。

(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
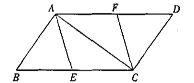
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com