
【题目】列方程解应用题
四川的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区。已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点。从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元。设从B地运往C处的蔬菜为![]() 吨。
吨。
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时![]() 的值?
的值?
C | D | 总计 | |
A | 200吨 | ||
B |
| 300吨 | |
总计 | 240吨 | 260吨 | 500吨 |
(2)已知总运费最小的调运费用是9280元,请你提交具体的调运方案.
【答案】(1)填表见解析;(2)具体的调运方案为:A基地的200吨蔬菜全部运到C安置点,再从B基地运40吨蔬菜到C安置点,剩余的260吨蔬菜全部运到D安置点。
【解析】
(1)调往C地蔬菜240吨,B地调往C地蔬菜![]() 吨,则A地调往C地(240
吨,则A地调往C地(240![]()
![]() )吨,
)吨,
因为A蔬菜基地有蔬菜200吨, A地调往C地(240![]()
![]() )吨,因此A地调往D地(
)吨,因此A地调往D地(![]()
![]() 40)吨,B蔬菜基地有蔬菜300吨, B地调往C地蔬菜
40)吨,B蔬菜基地有蔬菜300吨, B地调往C地蔬菜![]() 吨, 因此B地调往D地(300
吨, 因此B地调往D地(300![]()
![]() )吨,
)吨,
(2)因为从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元,所以可得:![]() ,解方程即可求解.
,解方程即可求解.
(1)
C | D | 总计 | |
A | 240 |
| 200吨 |
B |
| 300 | 300吨 |
总计 | 240吨 | 260吨 | 500吨 |
(2)解:根据题意,得:
![]() ,
,
![]() ,
,
所以,具体的调运方案为:A基地的200吨蔬菜全部运到C安置点,再从B基地运40吨蔬菜到C安置点,剩余的260吨蔬菜全部运到D安置点.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )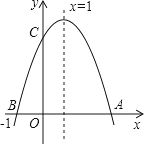
A.①④
B.①③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月29日,国家发改委批复了昌景黄铁路项目可行性研究报告.该项目位于赣皖两省,线路起自江西省南昌市南昌东站,经上饶市、景德镇市,安徽省黄山市,终至黄山北站.按照设计,行驶180千米,昌景黄高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少20分钟,求昌景黄高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
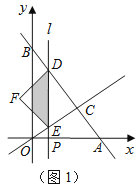
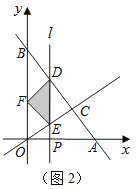
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,
交于点C(2,![]() ).平行于
).平行于![]() 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿![]() 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、![]() 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为![]() (秒).
(秒).
(1)求![]() 、
、![]() 的值;
的值;
(2)当![]() 为何值时,点F在
为何值时,点F在![]() 轴上(如图2);
轴上(如图2);
(3)设△DEF与△BCO重叠部分的面积为S,请求出S与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE. 
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD= ![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ![]() ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a= ![]() 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com