
【题目】已知二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=﹣3时,求二次函数图象的顶点坐标;
(2)当c=10时,若在函数值y=1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(3)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
【答案】
(1)解:当b=2,c=﹣3时,二次函数的解析式为y=x2+2x﹣3=(x+1)2﹣4,
故当x=﹣1时,二次函数取得最小值﹣4
(2)解:当c=10时,二次函数的解析式为y=x2+bx+10,
由题意得,x2+bx+10=1有两个相等是实数根,
∴△=b2﹣36=0,
解得b1=6,b2=﹣6,
∴二次函数的解析式y=x2+6x+10,y=x2﹣6x+10
(3)解:当c=b2时,二次函数解析式为y═x2+bx+b2,
图象开口向上,对称轴为直线x=﹣ ![]() ,
,
①当﹣ ![]() <b,即b>0时,
<b,即b>0时,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,
∴当x=b时,y=b2+bb+b2=3b2为最小值,
∴3b2=21,解得b1=﹣ ![]() (舍去),b2=
(舍去),b2= ![]() ;
;
②当b≤﹣ ![]() ≤b+3时,即﹣2≤b≤0,
≤b+3时,即﹣2≤b≤0,
∴x=﹣ ![]() ,y=
,y= ![]() b2为最小值,
b2为最小值,
∴ ![]() b2=21,解得b1=﹣2
b2=21,解得b1=﹣2 ![]() (舍去),b2=2
(舍去),b2=2 ![]() (舍去);
(舍去);
③当﹣ ![]() >b+3,即b<﹣2,
>b+3,即b<﹣2,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而减小,
故当x=b+3时,y=(b+3)2+b(b+3)+b2=3b2+9b+9为最小值,
∴3b2+9b+9=21.解得b1=1(舍去),b2=﹣4;
∴b= ![]() 时,解析式为:y=x2+
时,解析式为:y=x2+ ![]() x+7
x+7
b=﹣4时,解析式为:y=x2﹣4x+16.
综上可得,此时二次函数的解析式为y=x2+ ![]() x+7或y=x2﹣4x+16
x+7或y=x2﹣4x+16
【解析】(1)把b=2,c=﹣3代入函数解析式,求二次函数的最小值;(2)根据当c=10时,若在函数值y=l的情况下,只有一个自变量x的值与其对应,得到x2+bx+5=1有两个相等是实数根,求此时二次函数的解析式;(3)当c=b2时,写出解析式,分三种情况进行讨论即可.
【考点精析】掌握二次函数的最值是解答本题的根本,需要知道如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
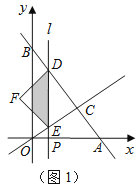
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,
交于点C(2,![]() ).平行于
).平行于![]() 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿![]() 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、![]() 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为![]() (秒).
(秒).
(1)求![]() 、
、![]() 的值;
的值;
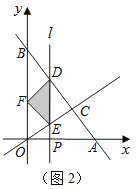
(2)当![]() 为何值时,点F在
为何值时,点F在![]() 轴上(如图2);
轴上(如图2);
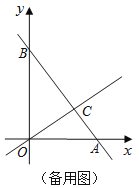
(3)设△DEF与△BCO重叠部分的面积为S,请求出S与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
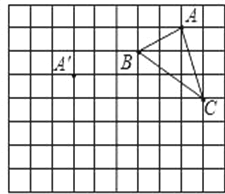
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,![]() 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将![]() 平移,使点A变换为点A′,点B′,C′,分别是B,C的对应点.
平移,使点A变换为点A′,点B′,C′,分别是B,C的对应点.
(1)请画出平移后的![]() ,并求
,并求![]() 的面积;
的面积;
(2)试说明△A'B'C'是如何由△ABC平移得到的;
(3)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:![]()
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com