
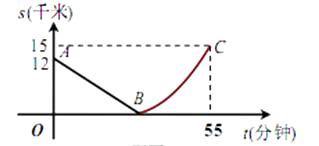
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
【答案】
(1)
解:11:40到12:10的时间是30分钟,则B(30,0),
潮头从甲地到乙地的速度=![]() =0.4(千米/分钟).
=0.4(千米/分钟).
(2)
解:∵潮头的速度为0.4千米/分钟,
∴到11:59时,潮头已前进19×0.4=7.6(千米),
∴此时潮头离乙地=12-7.6=4.4(千米),
设小红出发x分钟与潮头相遇,
∴0.4x+0.48x=4.4,
∴x=5,
∴小红5分钟后与潮头相遇.
(3)
解:把(30,0),C(55,15)代入s=![]() ,
,
解得b=![]() ,c=
,c=![]() ,
,
∴s=![]() .
.
∵v0=0.4,∴v=![]() ,
,
当潮头的速度达到单车最高速度0.48千米/分,即v=0.48时,
![]() =0.48,∴t=35,
=0.48,∴t=35,
∴当t=35时,s=![]() ,
,
∴从t=35分钟(12:15时)开始,潮头快于小红速度奔向丙地,小红逐渐落后,但小红仍以0.48千米/分的速度匀速追赶潮头.
设小红离乙地的距离为s1,则s1与时间t的函数关系式为s1=0.48t+h(t≥35),
当t=35时,s1=s=![]() ,代入得:h=
,代入得:h=![]() ,
,
所以s1=![]()
最后潮头与小红相距1.8千米时,即s-s1=1.8,
所以![]() ,,
,,
解得t1=50,t2=20(不符合题意,舍去)
∴t=50,
小红与潮头相遇后,按潮头速度与潮头并行到达乙地用时6分钟,
∴共需要时间为6+50-30=26分钟,
∴小红与潮头相遇到潮头离她1.8千米外共需26分钟.
【解析】(1)11:40到12:10的时间是30分钟,由图3可得甲乙两地的距离是12km,则可求出速度;
(2)此题是相遇问题,求出小红出发时,她与潮头的距离;再根据速度和×时间=两者的距离,即可求出时间;
(3)由(2)中可得小红与潮头相遇的时间是在12:04,则后面的运动过程为12:04开始,小红与潮头并行6分钟到12:10到达乙地,这时潮头开始从0.4千米/分加速到0.48千米/分钟,由题可得潮头到达乙后的速度为v=![]() , 在这段加速的过程,小红与潮头还是并行,求出这时的时间t1 , 从这时开始,写出小红离乙地关于时间t的关系式s1 , 由s-s1=1.8,可解出的时间t2(从潮头生成开始到现在的时间),所以可得所求时间=6+t2-30。
, 在这段加速的过程,小红与潮头还是并行,求出这时的时间t1 , 从这时开始,写出小红离乙地关于时间t的关系式s1 , 由s-s1=1.8,可解出的时间t2(从潮头生成开始到现在的时间),所以可得所求时间=6+t2-30。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=﹣3时,求二次函数图象的顶点坐标;
(2)当c=10时,若在函数值y=1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(3)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数 ![]() 的四个命题:①当
的四个命题:①当 ![]() 时,
时, ![]() 有最小值10;②
有最小值10;② ![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于 ![]() 时的函数值;③若
时的函数值;③若 ![]() ,且
,且 ![]() 是整数,当
是整数,当 ![]() 时,
时, ![]() 的整数值有
的整数值有 ![]() 个;④若函数图象过点
个;④若函数图象过点 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,则
,则 ![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
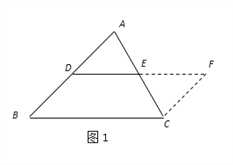
【题目】(1)方法回顾:在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在![]() 中,延长
中,延长![]() (
(![]() 分别是
分别是![]() 的中点)到点
的中点)到点![]() ,使得
,使得![]() ,连接
,连接![]() ;
;
第二步证明![]() ,再证四边形
,再证四边形![]() 是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)
是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)
(2)问题解决:如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.

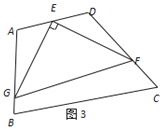
(3)拓展研究:如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 . 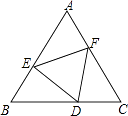
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com