
【题目】下列关于函数 ![]() 的四个命题:①当
的四个命题:①当 ![]() 时,
时, ![]() 有最小值10;②
有最小值10;② ![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于 ![]() 时的函数值;③若
时的函数值;③若 ![]() ,且
,且 ![]() 是整数,当
是整数,当 ![]() 时,
时, ![]() 的整数值有
的整数值有 ![]() 个;④若函数图象过点
个;④若函数图象过点 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,则
,则 ![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④
科目:初中数学 来源: 题型:
【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某粮库已存有粮食100吨,本周内粮库进出粮食的纪录如下(运进记为正,运出记为负):
![]()
(1)通过计算,说明本周内哪天粮库剩下的粮食最多?
(2)若运进的粮食为购进的,购买的价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
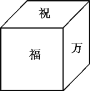
A. 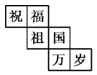 B.
B. 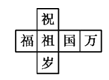 C.
C. 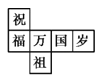 D.
D. 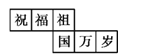
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com