
����Ŀ��ij�����Ѵ�����ʳ100�֣����������������ʳ�ļ�¼���£��˽���Ϊ�����˳���Ϊ������
![]()
��1��ͨ�����㣬˵����������������ʣ�µ���ʳ��ࣿ
��2�����˽�����ʳΪ�����ģ�����ļ۸�Ϊÿ��2000Ԫ���˳�����ʳΪ�����ģ������ļ۸�Ϊÿ��2300Ԫ�������ܵ�����Ϊ���٣�
��3����ÿ��ƽ����������ʳ������ͬ�����ٹ�������������ʳ�ɴﵽ200�֣�
���𰸡�������
��������
��1�����⡰+����ʾ���⣬��-����ʾ���⣬���ÿ�������������.
��2����һ�ܵ�����=������Ǯ��-�����Ǯ����������ʽ���㼴�����.
��3����200-һ��ǰ������ʳ��������ÿ��ƽ����������ʳ����-1����ʽ���㼴�����.
��1������һ100+35=135��
���ڶ�135-20=115��
������115-30=85��
������85+25=110��
������110-24=86��
������86+50=136��
������136-26=110��
����������࣬��136��.
��2��2300����20+30+24+26��-2000����35+25+50��
=2300��100-2000��110
=230000-220000
=10000Ԫ
��3����200-100������35+25+50-20-30-24-26��-1
=100��10-1
=10-1
=9��
���ٹ�9����������ʳ�ﵽ200��.


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Թ�˾���۲�Ϊ�˶����¸��µ����ۼƻ�����20λ����Ա���µ�������������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ������20λ������Ա������������ƽ��������λ���������ֱ��ǣ� ��
A.19��20��14
B.19��20��20
C.18.4��20��20
D.18.4��25��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��ں��� ![]() ���ĸ����⣺�ٵ�
���ĸ����⣺�ٵ� ![]() ʱ��
ʱ�� ![]() ����Сֵ10����
����Сֵ10���� ![]() Ϊ����ʵ����
Ϊ����ʵ���� ![]() ʱ�ĺ���ֵ����
ʱ�ĺ���ֵ���� ![]() ʱ�ĺ���ֵ������
ʱ�ĺ���ֵ������ ![]() ����
���� ![]() ����������
���������� ![]() ʱ��
ʱ�� ![]() ������ֵ��
������ֵ�� ![]() ������������ͼ�����
������������ͼ����� ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ����
���� ![]() �����������������ǣ� ��
�����������������ǣ� ��
A.��
B.��
C.��
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�����عˣ���ѧϰ��������λ��ʱ��Ϊ��̽����������λ�ߵ����ʣ�˼·���£�
��һ�����Ӹ����ߣ���ͼ1����![]() �У��ӳ�
�У��ӳ�![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣩����
���е㣩����![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��
�ڶ���֤��![]() ����֤�ı���
����֤�ı���![]() ��ƽ���ı��Σ��Ӷ��ó���������λ�ߵ����ʽ��ۣ�____________________________________������DE��BC��ʾ��
��ƽ���ı��Σ��Ӷ��ó���������λ�ߵ����ʽ��ۣ�____________________________________������DE��BC��ʾ��
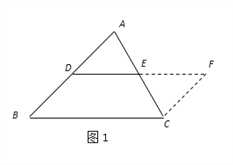
��2������������ͼ2����������ABCD�У�EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG��2��DF��3����GEF��90�㣬��GF�ij���

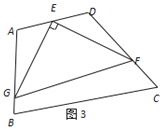
��3����չ�о�����ͼ3�����ı���ABCD�У���A��105�㣬��D��120�㣬EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG��![]() ��DF��2����GEF��90�㣬��GF�ij���
��DF��2����GEF��90�㣬��GF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩
��A��B��CΪ���������㣬�����C��A��B֮���ҵ�A�ľ����ǵ�C��B�ľ���3������ô���ǾͳƵ�C��{ A��B }����㣮
���磬��ͼ1����A��ʾ����Ϊ��3����B��ʾ����Ϊ1����ʾ0�ĵ�C����A�ľ�����3������B�ľ�����1����ô��C��{ A��B }����㣻���磬��ʾ��2�ĵ�D����A�ľ�����1������B�ľ�����3����ô��D�Ͳ���{A��B }����㣬����D��{B��A}����㣮
��֪ʶ���ã�
��ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ��3����N����ʾ����Ϊ5��
��1������ ������ʾ�ĵ���{ M��N}����㣻���� ������ʾ�ĵ���{N��M}����㣻
��2����ͼ3��A��BΪ���������㣬��A����ʾ����Ϊ��50����B����ʾ����Ϊ30������һ����P�ӵ�B���������˶��������Aֹͣ��P���˶��������ϵ�ʲôλ��ʱ��P��A��B��ǡ��һ����Ϊ�����������㣿
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��1��0��3����PΪ����������һ�������Ӧ����Ϊx��
![]()
��1��MN�ij�Ϊ ��
��2�������P����M����N�ľ����������ôx��ֵ�� ��
��3���������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����8����������ֱ��д��x��ֵ��������������˵��������
��4�������P��ÿ����1����λ���ȵ��ٶȴӵ�O�����˶���ͬʱ��M�͵�N�ֱ���ÿ����2����λ���Ⱥ�ÿ����3����λ���ȵ��ٶ�Ҳ�����˶�����t����ʱ��P����M����N�ľ����������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�GΪBC����һ�㣬BE��AG��E��DF��AG��F������DE��
��1����֤����ABE�ա�DAF��
��2����AF=1��S��ADE=8����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ѧС���������Ȼ�У�������������100ƪ�����������ȵķ���������Ϊ�������������黭��Ƶ���ֲ�ֱ��ͼ����ͼ������֪������5��С�����εĸߵı�Ϊl��3��7��6��3����ô����������б���Ϊ��������ģ��������ڻ����80��Ϊ���㣩��____ƪ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90�㣬D��BC�е㣬E��AD�е㣬��A��AF��BC

����֤����AEF�ա�DEB��
����֤���ı���ADCF�����Σ�
����AB=5��AC=4��������ADCF�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com