练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2,1）.一张透明纸上画有一个点和一条抛物线，平移透明纸，这个点与点A重合，此时抛物线的函数表达式为y=x2 ， 再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（ ）
    A.y=x2+8x+14
    B.y=x2-8x+14
    C.y=x2+4x+3
    D.y=x2-4x+3

    【答案】A
    【解析】解：如图，A（2,1），则可得C（-2，-1）.

    由A（2,1）到C（-2，-1），需要向左平移4个单位，向下平移2个单位，
    则抛物线的函数表达式为y=x2 ， 经过平移变为y=（x+4）2-2= x2+8x+14，
    故选A.
    题中的意思就是将抛物线y=x2平移后，点A平移到了点C，由A的坐标不难得出C的坐标，由平移的性质可得点A怎样平移到点C，那么抛物线y=x2 ， 就怎样平移到新的抛物线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．

    某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．

    思路：（1） 作AD⊥BC于D，设BD = x，用含x的代数式表示CD；（2）根据勾股定理，利用AD作为“桥梁”，建立方程模型，求出x；（3）利用勾股定理求出AD的长，再计算三角形面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句错误的有（ 　　）

    ①近似数0.010精确到千分位

    ②如果两个角互补，那么一个是锐角，一个是钝角

    ③若线段，则P一定是AB中点

    ④A与B两点间的距离是指连接A、B两点间的线段

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．

    求证：（1）△ABF≌△DCE；

    （2）△AOD是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

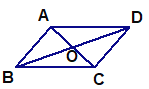
    【题目】如图，在四边形ABCD中，对角线AC、BD相交于点O，其中AC+BD=14，CD=5．

    (1)若四边形ABCD是平行四边形，则△OCD的周长为_____________；

    (2) 若四边形ABCD是矩形，则AD的长为_____________；

    (3) 若四边形ABCD是菱形，则菱形的面积为___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于函数 的四个命题：①当 时， 有最小值10；② 为任意实数， 时的函数值大于 时的函数值；③若 ，且 是整数，当 时， 的整数值有 个；④若函数图象过点 和 ，其中 ， ，则 ．其中真命题的序号是（ ）
    A.①
    B.②
    C.③
    D.④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据给出的数轴及已知条件，解答下面的问题：

    （1）已知点A，B，C表示的数分别为1，2.5，﹣3观察数轴，B，C两点之间的距离为　 　；

    与点A的距离为3的点表示的数是 ；

    （2）若将数轴折叠，使得A点与C点重合，则与B点重合的点表示的数是　 　；

    若此数轴上M，N两点之间的距离为2015（M在N的左侧），且当A点与C点重合时，M点与N点也恰好重合，则M，N两点表示的数分别是：M：　 　，N：　 　；

    （3）若数轴上P，Q两点间的距离为m（P在Q左侧），表示数n的点到P，Q两点的距离相等，则将数轴折叠，使得P点与Q点重合时，P，Q两点表示的数分别为：P：　 　，Q：　 （用含m，n的式子表示这两个数）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{ A，B }的奇点．

    例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{ A，B }的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B }的奇点，但点D是{B，A}的奇点．

    （知识运用）

    如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．

    （1）数　 　所表示的点是{ M，N}的奇点；数　 　所表示的点是{N，M}的奇点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，到达点A停止．P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校组织学生书法比赛，对参赛作品按A、B、C、D四个等级进行了评定．现随机抽取部分学生书法作品的评定结果进行分析，并绘制扇形统计图和条形统计图如下：

    根据上述信息完成下列问题：

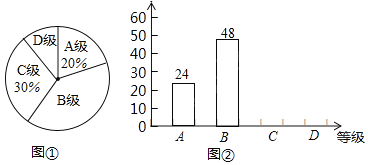
    （1）在这次抽样调查中，共抽查了多少名学生？

    （2）请在图②中把条形统计图补充完整；

    （3）求出扇形统计图中“D级”部分所对应的扇形圆心角的大小；

    （4）已知该校这次活动共收到参赛作品750份，请你估计参赛作品达到B级以上（即A级和B级）有多少份？

    查看答案和解析>>

    同步练习册答案