练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】顺次连接对角线相等的四边形的四边中点，所得的四边形一定是____________.

    【答案】菱形

    【解析】分析：作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=AC，GH=AC，HE=BD，FG=BD，再根据四边形的对角线相等可可知AC=BD，从而得到EF=FG=GH=HE，再根据四条边都相等的四边形是菱形即可得解．

    详解：如图，E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点，根据三角形的中位线定理，EF=AC，GH=AC，HE=BD，FG=BD，连接AC、BD．

    ∵四边形ABCD的对角线相等，∴AC=BD，所以，EF=FG=GH=HE，所以，四边形EFGH是菱形．

    故答案为：菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：

    请你根据上图填写下表：

    销售公司

    平均数

    方差

    中位数

    众数

    甲

    9

    乙

    9

    8

    请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：

    从平均数和方差结合看；

    从折线图上甲、乙两个汽车销售公司销售数量的趋势看分析哪个汽车销售公司较有潜力．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．

    求证：（1）△ABF≌△DCE；

    （2）△AOD是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于函数 的四个命题：①当 时， 有最小值10；② 为任意实数， 时的函数值大于 时的函数值；③若 ，且 是整数，当 时， 的整数值有 个；④若函数图象过点 和 ，其中 ， ，则 ．其中真命题的序号是（ ）
    A.①
    B.②
    C.③
    D.④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据给出的数轴及已知条件，解答下面的问题：

    （1）已知点A，B，C表示的数分别为1，2.5，﹣3观察数轴，B，C两点之间的距离为　 　；

    与点A的距离为3的点表示的数是 ；

    （2）若将数轴折叠，使得A点与C点重合，则与B点重合的点表示的数是　 　；

    若此数轴上M，N两点之间的距离为2015（M在N的左侧），且当A点与C点重合时，M点与N点也恰好重合，则M，N两点表示的数分别是：M：　 　，N：　 　；

    （3）若数轴上P，Q两点间的距离为m（P在Q左侧），表示数n的点到P，Q两点的距离相等，则将数轴折叠，使得P点与Q点重合时，P，Q两点表示的数分别为：P：　 　，Q：　 （用含m，n的式子表示这两个数）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)方法回顾：在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：

    第一步添加辅助线：如图1，在中，延长（分别是的中点）到点，使得，连接；

    第二步证明，再证四边形是平行四边形，从而得出三角形中位线的性质结论：____________________________________（请用DE与BC表示）


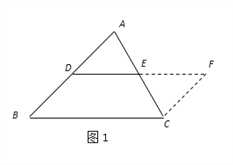
    （2）问题解决：如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．

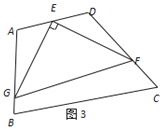
    （3）拓展研究：如图3，在四边形ABCD中，∠A＝105°，∠D＝120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝，DF＝2，∠GEF＝90°，求GF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{ A，B }的奇点．

    例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{ A，B }的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B }的奇点，但点D是{B，A}的奇点．

    （知识运用）

    如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．

    （1）数　 　所表示的点是{ M，N}的奇点；数　 　所表示的点是{N，M}的奇点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，到达点A停止．P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．

    （1）求证：△ABE≌△DAF；

    （2）若AF=1，S△ADE=8，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

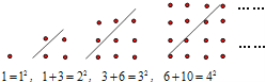
    【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”，而把1、4、9、16 …这样的数称为“正方形数”．从下图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．用等式表示第100个正方形点阵中的规律_________________.

    查看答案和解析>>

    同步练习册答案