
【题目】如图1,点A、B分别在数轴原点O的左右两侧,且 ![]() OA+50=OB,点B对应数是90.
OA+50=OB,点B对应数是90. ![]()
(1)求A点对应的数;
(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离; ![]()
(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值. ![]()
【答案】
(1)解:如图1,∵点B对应数是90,
∴OB=90.
又∵ ![]() OA+50=OB,即
OA+50=OB,即 ![]() OA+50=90,
OA+50=90,
∴OA=120.
∴点A所对应的数是﹣120
![]()
(2)解:依题意得,MN=|(﹣120+7t)﹣2t|=|﹣120+5t|,
PM=|2t﹣(90﹣8t)|=|10t﹣90|,
又∵MN=PM,
∴|﹣120+5t|=|10t﹣90|,
∴﹣120+5t=10t﹣90或﹣120+5t=﹣(10t﹣90)
解得t=﹣6或t=14,
∵t≥0,
∴t=14,点M、N之间的距离等于点P、M之间的距离
![]()
(3)解:依题意得RQ=( 45+4t)﹣(﹣60﹣4.5t)=105+8.5t,
RO=45+4t,
PN=(90+8t)﹣(﹣120﹣7t)=210+15t,
则22RQ﹣28RO﹣5PN=22(105+8.5t)﹣28(45+4t)﹣5(210+15t)=0
![]()
【解析】(1)根据点B对应的数求得OB的长度,结合已知条件和图形来求点A所对应的数;(2)由M、N之间的距离等于P、M之间的距离列式为,列方程求出t;(3)由M、N之间的距离等于P、M之间的距离列式为,列方程求出t,并求出RQ,RO及PN,再求出22RQ﹣28RO﹣5PN的值.
【考点精析】根据题目的已知条件,利用数轴和两点间的距离的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.
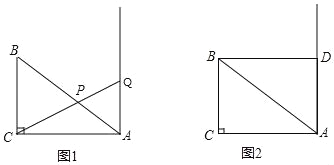
(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球上的海洋面积约三亿六千一百万平方千米,用科学记数法表示为( )平方千米.
A. 361×106B. 36.1×107C. 3.61×108D. 0.361×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com