
已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=![]() ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
(1)求⊙O的半径;
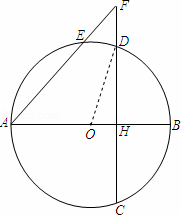
(2)如图,当点E在AD上时,求y与x之间的函数解析式,并写出函数的定义域;
(3)如果EF=![]() ,求DF的长.
,求DF的长.
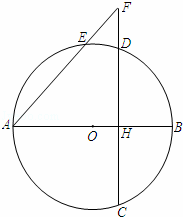
解答: 解:(1)连接OD,设⊙O的半径OA=OD=r,
∵AB是⊙O的直径,弦CD⊥AB,
∴DH=![]() DC=
DC=![]() ×4
×4![]() =2
=2![]() ,
,
在Rt△OHD中,∵OD2﹣OH2=DH2,OH2=(AH﹣OA)2=(5﹣r)2,
∴r2﹣(5﹣r)2=(2![]() )2,解得r=
)2,解得r=![]() ,
,
∴⊙O的半径为![]() ;
;
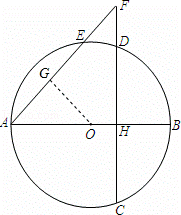
(2)作OG⊥AE,垂足为G,如图,
∴AG=![]() AE=
AE=![]() x,
x,
∴△AOG∽△AFH,
∴AG:AH=AO:AF,即![]() x:5=
x:5=![]() :AF,解得AF=
:AF,解得AF=![]() ,
,
∴FH=![]() =
=![]() =
=![]()
![]() ,
,
∵DF=FH﹣DH,
∴y关于x的函数解析式为y=![]()
![]() ﹣2
﹣2![]() ,
,
定义域为0<x≤3![]() ;
;
(3)当点E在弧AD上时,如图,∵AF﹣AE=EF,即![]() ﹣x=
﹣x=![]() ,
,
化为整式方程得2x2+3x﹣90=0,解得x1=﹣![]() (舍去),x2=6,
(舍去),x2=6,
∴DF=y=![]()
![]() ﹣2
﹣2![]() =
=![]() ;
;
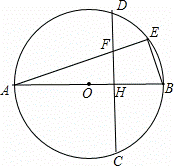
当点E在弧DB上时,如图,∵AE﹣AF=EF,即x﹣![]() =
=![]() ,
,
化为整式方程得2x2﹣3x﹣90=0,解得x1=![]() ,x2=6(舍去),
,x2=6(舍去),
∵AB为直径,
∴∠E=90°,
∴△AHF∽△AEB,BE=![]() =
=![]() ,
,
∴FH:BE=AH:AE,即FH:![]() =5:
=5:![]() ,解得FH=
,解得FH=![]()
∴DF=DH﹣FH=2![]() ﹣
﹣![]()
当点E在BC弧上时,同上得FH=![]() ,
,
∴DF=DH+FH=2![]() +
+![]() .
.


科目:初中数学 来源: 题型:
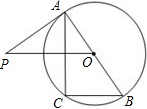 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.| 7 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
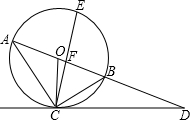
 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A, |
| EC |
 |
| CB |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com