
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上.
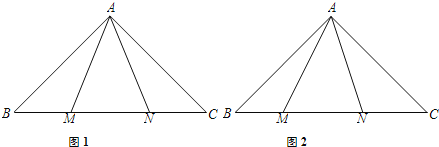
(1)如图1,如果AM=AN,求证:BM=CN;
(2)如图2,如果M、N是边BC上任意两点,并满足∠MAN=45°,那么线段BM、MN、NC是否有可能使等式MN2=BM2+NC2成立?如果成立,请证明;如果不成立,请说明理由.
【答案】见解析
【解析】
试题(1)根据已知条件“在Rt△ABC中,∠BAC=90°,AB=AC”以及等腰直角三角形的性质来判定△ABM≌△CAN(AAS);然后根据全等三角形的对应边相等求得BM=CN;
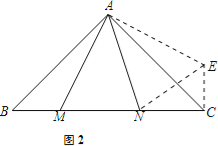
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.通过证明△ABM≌△ACE(SAS)推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE;然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°,所以△MAN≌△EAN(SAS),故全等三角形的对应边MN=EN;最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2.
(1)证明:∵AB=AC,∴∠B=∠C.
∵AM=AN,∴∠AMN=∠ANM.
即得∠AMB=∠ANC.(1分)
在△ABM和△CAN中,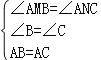
∴△ABM≌△CAN(AAS).(2分)
∴BM=CN.(1分)
另证:过点A作AD⊥BC,垂足为点D.
∵AB=AC,AD⊥BC,∴BD=CD.(1分)
同理,证得MD=ND.(1分)
∴BD﹣MD=CD﹣ND.
即得BM=CN.(2分)
(2)MN2=BM2+NC2成立.
证明:过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.(1分)
在△ABM和△ACE中,
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.(2分)
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.(1分)
在△MAN和△EAN中,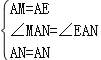
∴△MAN≌△EAN(SAS).
∴MN=EN.(1分)
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
即得MN2=BM2+NC2.(1分)
另证:由∠BAC=90°,AB=AC,可知,把△ABM绕点A逆时针旋转90°后,AB与AC重合,设点M的对应点是点E.
于是,由图形旋转的性质,得AM=AE,∠BAM=∠CAE.(3分)
以下证明同上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是 . 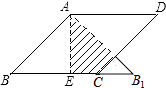
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点. 
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)如图②,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图③,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE与△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
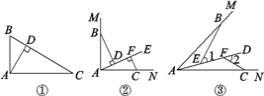
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com