
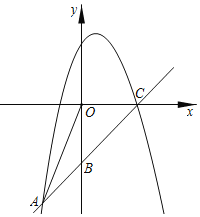
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣1,﹣5),B(0,﹣4)两点且与x轴交于点C,二次函数y=ax2+bx+4的图象经过点A、点C.
(1)求一次函数和二次函数的函数表达式;
(2)连接OA,求∠OAB的正弦值;
(3)若点D在x轴的正半轴上,是否存在以点D,C,B构成的三角形与△OAB相似?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)y=x﹣4,y=﹣2x2+7x+4;(2)![]() ;(3)存在,(6,0)或(20,0)
;(3)存在,(6,0)或(20,0)
【解析】
(1)利用待定系数法求出一次函数的解析式,然后根据与x轴的交点y=0,求出C的坐标,然后根据A与C的坐标求出二次函数的解析式即可;
(2)过O作OH⊥BC,垂足为H,证明△BOC为等腰直角三角形,求出OH=![]() BC=2
BC=2![]() ,然后求出OA,即可求出∠OAB的正弦值;
,然后求出OA,即可求出∠OAB的正弦值;
(3)利用勾股定理求出AH,再求出AB=![]() ,然后分情况求出D点的坐标即可.
,然后分情况求出D点的坐标即可.
解:(1)∵一次函数y=kx+b的图象经过A(﹣1,﹣5),B(0,﹣4)两点,
∴﹣5=﹣k+b,b=﹣4,k=1,
∴一次函数解析式为:y=x﹣4,
∵一次函数y=x﹣4与x轴交于点C,
∴y=0时,x=4,
∴C(4,0),
∵二次函数y=ax2+bx+4的图象经过点A(﹣1,﹣5)、点C(4,0),
∴![]() ,
,
解得a=﹣2,b=7,
∴二次函数的函数表达式为y=﹣2x2+7x+4;
(2)过O作OH⊥BC,垂足为H,
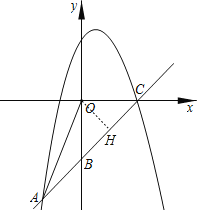
∵C(4,0),B(0,﹣4),
∴OB=OC=4,即△BOC为等腰直角三角形,
∴BC=![]() =
=![]() =4
=4![]() ,
,
∴OH=![]() BC=2
BC=2![]() ,
,
由点O(0,0),A(﹣1,﹣5),得:OA=![]() ,
,
在Rt△OAH中,sin∠OAB=![]() =
=![]() =
=![]() ;
;
(3)存在,
由(2)可知,△OBC为等腰直角三角形,OH=BH=2![]() ,
,
在Rt△AOH中,根据勾股定理得:AH=![]() =
=![]() =3
=3![]() ,
,
∴AB=AH﹣BH=![]() ,
,
∴当点D在C点右侧时,∠OBA=∠DCB=135°,
①当![]() ,即
,即![]() 时,解得CD=2,
时,解得CD=2,
∵C(4,0),即OC=4,
∴OD=OC+CD=2+4=6,
此时D坐标为(6,0);
②当![]() ,即
,即![]() 时,
时,
解得CD=16,
∵C(4,0),即OC=4,∴OD=OC+CD=16+4=20,
此时D坐标为(20,0),
综上所述,若△BCD与△ABO相似,此时D坐标为(6,0)或(20,0).


科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=8,AD=6, 点E是边CD上一个动点,连接AE,将△AED沿直线AE翻折得△AEF.
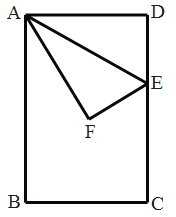
(1) 当点C落在射线AF上时,求DE的长;
(2)以F为圆心,FB长为半径作圆F,当AD与圆F相切时,求cos∠FAB的值;
(3)若P为AB边上一点,当边CD上有且仅有一点Q满∠BQP=45°,直接写出线段BP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.
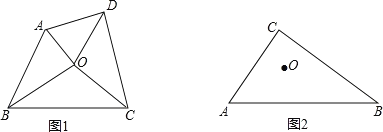
(1)试举出一个有内心的四边形.
(2)如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.
(3)如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC、BC于点D.E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.
(4)问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.据统计,当每辆车的月租金为3000元时,可全部租出.每辆车的月租金每增加50元时,未租出的车将会增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的租金定为多少元时,租赁公司的月收益(租金收入扣除维护费)可达到306600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
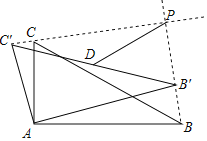
【题目】如图,将水平放置的三角板ABC绕直角顶点A逆时针旋转,得到△AB'C',连结并延长BB'、C'C相交于点P,其中∠ABC=30°,BC=4.
(1)若记B'C'中点为点D,连结PD,则PD=_____;
(2)若记点P到直线AC'的距离为d,则d的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BF平分∠ABC交AD于点F,CE平分∠DCB交AD于点E,BF和CE相交于点P.

(1)求证:AE=DF.
(2)已知AB=4,AD=5.
①求![]() 的值;
的值;
②求四边形ABPE的面积与△BPC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com