
 在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.
在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.分析 (1)根据$\sqrt{m+3n}$+(n-6)2=0,运用非负数的性质,得出m,n的值,即可求得B,C两点坐标;
(2)分两种情况:①当点D在线段BH上时,作HF∥PD,则HF∥AC,求得∠AHP=∠DPH+∠CAH;②当D在线段CH上时,作HF∥PD,则HF∥AC,求得∠AHP=∠CAH-∠DPH;
(3)先过P作PG⊥AH于G,根据△APG∽△ABH,求得PG=18-6t,再分两种情况:①当Q在线段CH上时,②当Q在线段BH上时,分别根据S△AHP=4S△AHQ,求得t的值和点Q的坐标.
解答 解:(1)∵$\sqrt{m+3n}$+(n-6)2=0,
∴$\left\{\begin{array}{l}{m+3n=0}\\{n-6=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-18}\\{n=6}\end{array}\right.$,
∴B(-18,-2$\sqrt{3}$),C(6,-2$\sqrt{3}$);
(2)∠AHP=∠DPH+∠CAH或∠AHP=∠CAH-∠DPH.
分两种情况:
①如图所示,当点D在线段BH上时,作HF∥PD,则HF∥AC,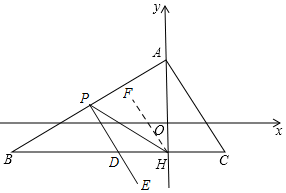
∴∠DPH=∠FHP,∠CAH=∠FHA,
∵∠AHP=∠FHP+∠FHA,
∴∠AHP=∠DPH+∠CAH;
②如图所示,当D在线段CH上时,作HF∥PD,则HF∥AC,
∴∠DPH=∠FHP,∠CAH=∠FHA,
∵∠AHP=∠FHA-∠FHP,
∴∠AHP=∠CAH-∠DPH;
(3)由题可得,BP=4$\sqrt{3}$t,AP=12$\sqrt{3}$-4$\sqrt{3}$t,CQ=3t,CH=6,BH=18,
过P作PG⊥AH于G,而BC⊥AO,
∴PG∥BC,
∴△APG∽△ABH,
∴$\frac{AP}{AB}$=$\frac{PG}{BH}$,即$\frac{12\sqrt{3}-4\sqrt{3}t}{12\sqrt{3}}$=$\frac{PG}{18}$,
∴PG=18-6t,
分两种情况:
①当Q在线段CH上时,HQ=6-3t,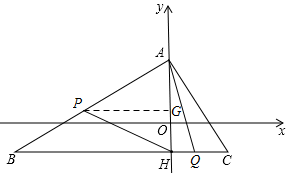
∵S△AHP=4S△AHQ,
∴$\frac{1}{2}$×AH×PG=4×$\frac{1}{2}$×AH×HQ,即PG=4HQ,
∴18-6t=4×(6-3t),
解得t=1,
此时HQ=6-3=3,
∴Q(3,-2$\sqrt{3}$);
②当Q在线段BH上时,HQ=3t-6,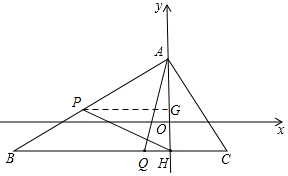
∵S△AHP=4S△AHQ,
∴$\frac{1}{2}$×AH×PG=4×$\frac{1}{2}$×AH×HQ,即PG=4HQ,
∴18-6t=4×(3t-6),
解得t=$\frac{7}{3}$,
此时,HQ=7-6=1,
∴Q(-1,-2$\sqrt{3}$),
综上所述,当t=1时,S△AHP=4S△AHQ,Q(3,-2$\sqrt{3}$);当t=$\frac{7}{3}$时,S△AHP=4S△AHQ,Q(-1,-2$\sqrt{3}$).
点评 本题属于三角形综合题,主要考查了非负数的性质,平行线的性质,相似三角形的判定与性质以及三角形的面积的综合应用,解决问题的关键是作辅助线构造平行线,运用分类讨论思想进行计算求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
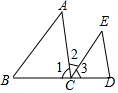 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
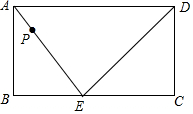 如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
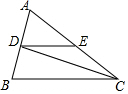 如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm.
如图,已知在△ABC中,CD平分∠ACB,且CD⊥AB于D,DE∥BC交AC于点E,AC=3cm,AB=2cm,则△ADE的周长为4cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com