解:(1)4t,

(2)①当点P、M、N在同一直线上时,PM+MN的值最小.
如图,在Rt△APM中,易知
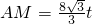
,
又∵
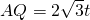
,
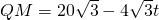
.
由AQ+QM=AM得:
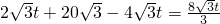
,
解得
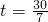
.
∴当
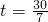
时,PM+MN的值最小.…

②如图1,若0<t≤5时,则AP=4t,
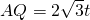
.
则

,
又∵
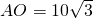
,AB=20,
∴
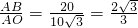
.
∴
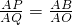
.
又∵∠CAB=30°,
∴△APQ∽△ABO.
∴∠AQP=90°,即PQ⊥AC.
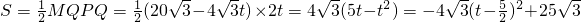
,
当

时,S有最大值
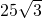
.
②若5<t≤10时,则CP=40-4t,PQ=20-2t,
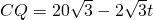
.
则
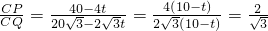
,
又∵
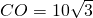
,CB=20,
∴
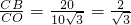
.
又∵∠ACB=30°,
∴△QCP∽△OCB.
∴∠CQP=90°,即PQ⊥AC
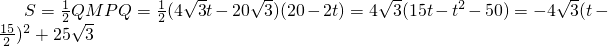
,
当
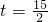
时,S有最大值
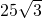
.
综上,当

或

时,S的最大值都是
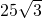
.
分析:(1)根据点P以4cm/s的速度,沿A→B→C的路线向点C运动;点Q以
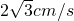
的速度,沿A→C的路线向点C运动,于是在时间t内即可求出两点运动的位移,即可求出AP和AQ的长度.
(2)①当点P、M、N在同一直线上时,PM+MN的值最小,根据AQ+QM=AM即可求出t的值,如图1,若0<t≤5时,则AP=4t,
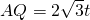
,根据三角形相似证明∠AQP=90°,即PQ⊥AC,于是求出△PQM的面积S的最大值,同理求出当5<t≤10时,△PQM的面积S的最大值.
点评:本题主要考查相似三角形的性质与判定、三角函数的最值等知识点,解答本题的关键是熟练掌握相似三角形的性质,此题是一道综合性比较强的习题,难度有点大.

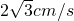 的速度,沿A→C的路线向点C运动.
的速度,沿A→C的路线向点C运动.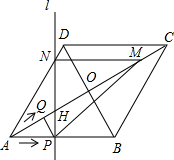 当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
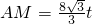 ,
,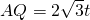 ,
,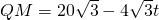 .
.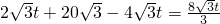 ,
,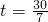 .
.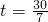 时,PM+MN的值最小.…
时,PM+MN的值最小.…
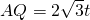 .
. ,
,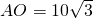 ,AB=20,
,AB=20,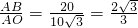 .
.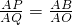 .
.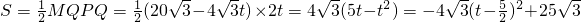 ,
, 时,S有最大值
时,S有最大值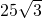 .
.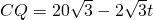 .
.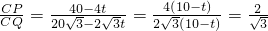 ,
,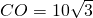 ,CB=20,
,CB=20,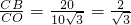 .
.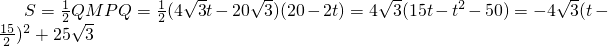 ,
,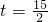 时,S有最大值
时,S有最大值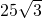 .
. 或
或 时,S的最大值都是
时,S的最大值都是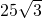 .
.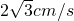 的速度,沿A→C的路线向点C运动,于是在时间t内即可求出两点运动的位移,即可求出AP和AQ的长度.
的速度,沿A→C的路线向点C运动,于是在时间t内即可求出两点运动的位移,即可求出AP和AQ的长度.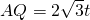 ,根据三角形相似证明∠AQP=90°,即PQ⊥AC,于是求出△PQM的面积S的最大值,同理求出当5<t≤10时,△PQM的面积S的最大值.
,根据三角形相似证明∠AQP=90°,即PQ⊥AC,于是求出△PQM的面积S的最大值,同理求出当5<t≤10时,△PQM的面积S的最大值.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案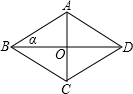 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( ) 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.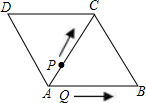 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).