练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若单项式5x4y和25xnym是同类项，则m+n的值为 ．

    【答案】5
    【解析】解：∵单项式5x4y和25xnym是同类项，
    ∴n=4，m=1，
    ∴m+n=4+1=5．
    故填：5．
    根据同类项的定义中相同字母的指数也相同，得出m、n的值，即可求出m+n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】方程x-2=2-x的解是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中俄“海上联合—2014”反潜演习中，我军舰A测得潜艇C的俯角为300．位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680，试根据以上数据求出潜艇C离开海平面的下潜深度。（结果保留整数。参考数据:sin680≈0．9，cos680≈0．4，，tan680≈2．5． ≈1．7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】不等式x﹣2≤0的解集是（　　）

    A. x＞2 B. x＜2 C. x≥2 D. x≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】买一个足球需要m元，买一个篮球需要n元，则买4个足球、7个篮球共需要（ ）
    A.（7m+4n）元
    B.28mn元
    C.（4m+7n）元
    D.11mn元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据等式和不等式的性质，可以得到：若a﹣b＞0，则a＞b；若a﹣b=0，则a=b；若a﹣b＜0，则a＜b．这是利用“作差法”比较两个数或两个代数式值的大小．
    （1）试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系；
    解：（5m2﹣4m+2）﹣（4m2﹣4m﹣7）=5m2﹣4m+2﹣4m2+4m+7=m2+9，因为m2≥0
    所以m2+9＞0
    所以5m2﹣4m+24m2﹣4m﹣7．（用“＞”或“＜”填空）
    （2）已知A=5m2﹣4（ m﹣ ），B=7（m2﹣m）+3，请你运用前面介绍的方法比较代数式A与B的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，∠A=30°．
    （1）如图①，∠ABC、∠ACB的角平分线交于点O，则∠BOC=°．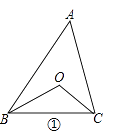
    （2）如图②，∠ABC、∠ACB的三等分线分别对应交于O1、O2 ， 则∠BO2C=°．
    （3）如图③，∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1（内部有n﹣1个点），求∠BOn﹣1C（用n的代数式表示）．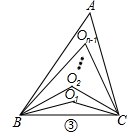
    （4）如图③，已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 ， 若∠BOn﹣1C=60°，求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“一带一路”贯穿欧亚大陆，东边连接亚太经济圈，西边进入欧洲经济圈，大致涉及65个国家，总人口44亿，生产总值23万亿美元．将23万用科学记数法表示应为(　　)

    A. 23×104B. 2.3×105C. 2.3×104D. 0.23×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：

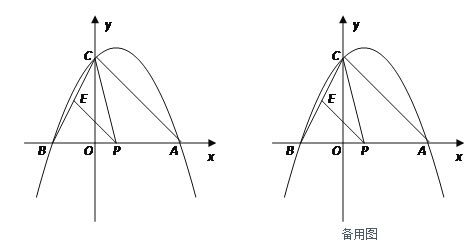
    【题目】如图，抛物线与x轴交于A(x1，0)、B(x2，0)两点，且x1＞x2，与y轴交于点C(0，4)，其中x1、x2是方程x2－2x－8＝0的两个根．

    (1)求这条抛物线的解析式；

    (2)点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；

    (3)探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三角形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案