
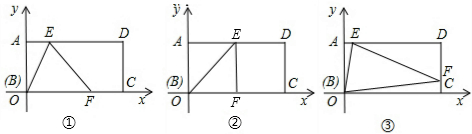
分析 (I)由“折痕三角形”的定义,利用折叠的性质可得结论;
(II)根据“折痕三角形”的定义,利用垂直平分线的性质可得四边形ABEF为正方形,由正方形的性质得BF=AB,易得点F的坐标;
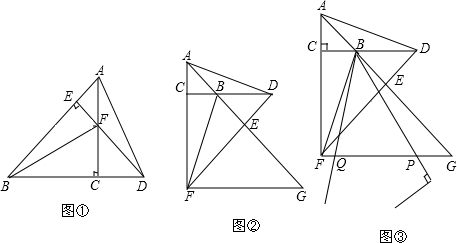
(III)利用分类讨论的思想结合图形,当F在BC上时,如图②所示,利用矩形面积得三角形面积的最大值;当F在CD上时,如图③所示,过F作FH∥BC交AB于点H,交BE于K,利用三角形的面积公式和矩形的面积得三角形面积的最大值;求面积最大时,点E的坐标,结合图形,利用勾股定理可得ED的长,得点E的坐标;当F在DC中点时,点E与点A重合,如图⑤所示易得点E.
解答 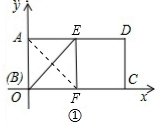 解:(I)由折叠的定义可知,△BEF为矩形ABCD的“折痕三角形”时,BF=EF,
解:(I)由折叠的定义可知,△BEF为矩形ABCD的“折痕三角形”时,BF=EF,
∴△BEF是等腰三角形.
故答案为:等腰;
(II)如图②所示,
∵折痕垂直平分BE,AB=AE=2,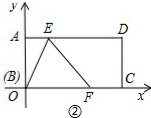 ∴点A在BE的垂直平分线上,即折痕经过点A,
∴点A在BE的垂直平分线上,即折痕经过点A,
∴四边形ABEF为正方形,
∴BF=AB=2,
∴点F的坐标为(2,0);
(III)矩形ABCD存在面积最大的折痕△BEF,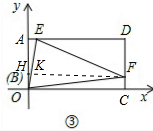
(1)当F在BC上时,如图②所示,
S△BEF≤$\frac{1}{2}$S矩形ABCD,即当F与C重合时,面积最大为4;
(2)当F在CD上时,如图③所示,
过F作FH∥BC交AB于点H,交BE于K,
∵S△EKF=$\frac{1}{2}$KF•AH$≤\frac{1}{2}HF•AH$=$\frac{1}{2}$S矩形AHFD,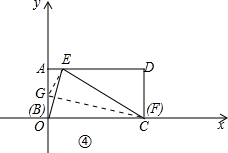 S△BKF=$\frac{1}{2}$KF•BH≤$\frac{1}{2}$HF•BH=$\frac{1}{2}$S矩形BCFH,
S△BKF=$\frac{1}{2}$KF•BH≤$\frac{1}{2}$HF•BH=$\frac{1}{2}$S矩形BCFH,
∴S△BEF=S△EKF+S△BKF≤$\frac{1}{2}$S矩形AHFD+$\frac{1}{2}$S矩形BCFH=$\frac{1}{2}$S矩形ABCD=4,
即当F为CD的中点时,△BEF的面积最大为4;
下面求面积最大时,点E的坐标,
(1)当F与点C重合时,如图④所示,由折叠可知:CE=CB=4,
在Rt△CDE中,ED=$\sqrt{C{D}^{2}{-CE}^{2}}$=$\sqrt{{4}^{2}{-2}^{2}}$=2$\sqrt{3}$,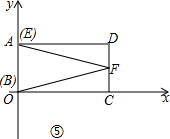 ∴AE=$4-2\sqrt{3}$,
∴AE=$4-2\sqrt{3}$,
∴点E的坐标(4-2$\sqrt{3}$,2);
(2)当F在DC中点时,点E与点A重合,如图⑤所示,此时E(0,2),
综上所述,折痕△BEF的最大面积为4时,点E的坐标为(0,2)或(4-2$\sqrt{3}$,2).
点评 本题主要考查了折叠的性质,正方形的性质,三角形的面积公式等,数形结合,分类讨论是解答此题的关键.


科目:初中数学 来源: 题型:选择题
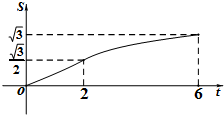 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )| A. | 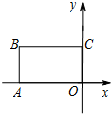 | B. | 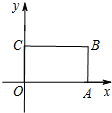 | C. | 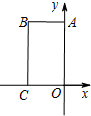 | D. | 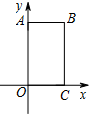 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
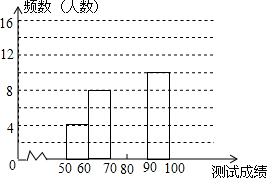 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
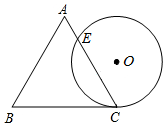 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
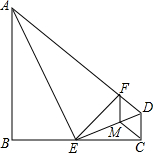 已知四边形ABCD中,∠ABC=90°,AB∥CD,BC=12,AB>6,点E为BC的中点,连接AE,ED,△ABE与△AFE关于直线AE对称,且点F在AD上
已知四边形ABCD中,∠ABC=90°,AB∥CD,BC=12,AB>6,点E为BC的中点,连接AE,ED,△ABE与△AFE关于直线AE对称,且点F在AD上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com