
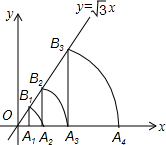
 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$). 分析 先根据一次函数方程式求出B1点的坐标,再根据B1点的坐标求出A2点的坐标,得出B2的坐标,以此类推总结规律便可求出点B6的坐标.
解答 解:直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交 直线于点B1可知B1点的坐标为(1,$\sqrt{3}$),
以原O为圆心,OB1长为半径画弧x轴于点A2,OA2=OB1,
OA2=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,点A2的坐标为(2,0),
这种方法可求得B2的坐标为(2,2$\sqrt{3}$),故点A3的坐标为(4,0),B3(4,4$\sqrt{3}$)
以此类推便可求出点B6的坐标为(32,32$\sqrt{3}$).
故答案为(32,32$\sqrt{3}$).
点评 本题主要考查了一次函数图象上点的坐标特征,做题时要注意数形结合思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.


科目:初中数学 来源: 题型:填空题
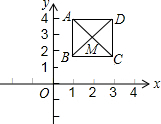 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
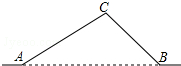 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
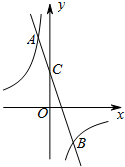 如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com