练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．（-2）2=4，2-2=$\frac{1}{4}$，（-2）-2=$\frac{1}{4}$．

    分析 根据有理数的乘法以及负整数指数幂的性质进行计算即可．

    解答 解：（-2）2=4；
    2-2=$\frac{1}{{2}^{2}}=\frac{1}{4}$；
    （-2）-2=$\frac{1}{（-2）^{2}}=\frac{1}{4}$．
    故答案为：4；$\frac{1}{4}$；$\frac{1}{4}$．

    点评 本题主要考查的是有理数的乘方和负整数指数幂的运算，掌握有理数的乘方和负整数指数幂的运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

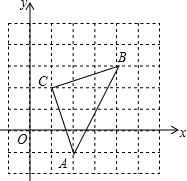    6．如图，直角坐标系中，△ABC的顶点都在网格点上，其中，A点坐标为（2，-1）．
    （1）写出B、C点的坐标：B（4，3）、C（1，2）；
    （2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，画出图形并写出A′、B′、C′的三点坐标；
    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-3（x-1）＜8-x}\end{array}\right.$，并把其解集在数轴上表示出来．
    （2）已知x，y满足（2014-x）2+|y-2015|=0，求[（x-y）2+（x+y）（x-y）]÷2x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

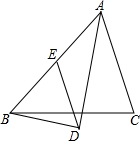    4．在△ABC中，AD平分∠BAC．BD⊥AD，垂足为D，过D作DE∥AC，交AB于E．
    （1）求证：AE=DE；
    （2）若AB=8，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

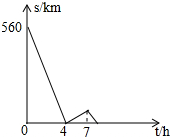    11．一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后分别按原速同时驶往甲地，两车之间的距离S（km）与慢车行驶时间t（h）之间的函数图象如图所示，下列说法：
    ①甲、乙两地之间的距离为560km；
    ②快车速度是慢车速度的1.5倍；
    ③快车到达甲地时，慢车距离甲地60km；
    ④相遇时，快车距甲地320km
    其中正确的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．对于反比例函数y=$\frac{1}{x}$，下列说法正确的是（　　）
    A．图象经过点（1，-1）B．图象位于第二、四象限
    C．当x＜0时，y随x增大而增大D．图象是中心对称图形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．2x6y2•x3y+（-25x8y2）（-xy）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某市招聘教师，对应聘者分别进行教学能力、科研能力、组织能力三项测试，其中甲、乙两人的成就如下表：（单位：分）
    项目
    人员    		教学能力科研能力组织能力
    甲869373
    乙819579
    （1）根据实际需要，将阅读能力、科研能力、组织能力三项测试得分按5：3：2的比确定最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
    （2）按照（1）中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图（每组分数段均包含左端数值，不包含右端数值），并决定由高分到低分录用8人．甲、乙两人能否被录用？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知等边△ABC中，AB=8，D为AB上一点，BD=2，E为BC上一点（E不与点B和C重合）
    （1）作∠DEF=60°，交AC于点F，如图1
    ①若BE=2，求CF的长
    ②设BE=x，CF=y，试求y关于x的函数关系式并求y的取值范围；
    （2）如图2，若BE=6，过A、D、E三点作圆交AC于点G，试求CG的长．

    查看答案和解析>>

    同步练习册答案