

���� ��1�����������DZ�ʾ����ֱ�ߣ����������ϵĵ��ʾ����
��2�������������ļ����;���ֵ�����ʣ��ɵô𰸣�
��3�����ݵ�λ������������ʻ·�̣��ɵú�������
��� �⣺��1����A��B��C��ͼ��ʾ��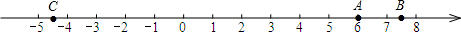
��2��AC=|6-��-4.5��|=10.5��ǧ�ף���
�ʳ���A�����C���10.5ǧ�ף�
��3��6+1.5+12+4.5=24��ǧ�ף���
24��0.08=1.92��1.9��������
��С��һ�Ҵӳ��������ؼ�������·��С���ĺ�����ԼΪ1.9����
���� ���⿼�����������ļӼ��������Ӧ�ã��ؼ����ܸ��������г���ʽ�����еڣ�3��С����С�γ���ʻ��·���ǴӼ�����������У��ٵ�үү�ң��ٴ�үү�ҵ���ң����Ϸ��ؼ����·�̺ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
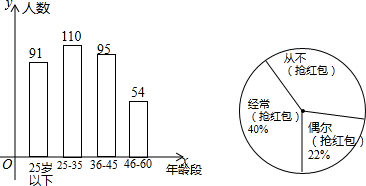
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
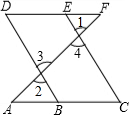 ��ͼ��EΪDF�ϵĵ㣬BΪAC�ϵĵ㣬��1=��2����C=��D����ôDF��AC��
��ͼ��EΪDF�ϵĵ㣬BΪAC�ϵĵ㣬��1=��2����C=��D����ôDF��AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
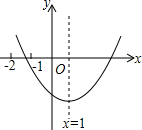 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���b2-4ac��0����abc��0����9a+3b+c��0�����У���ȷ���۵ĸ����ǣ�������
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���b2-4ac��0����abc��0����9a+3b+c��0�����У���ȷ���۵ĸ����ǣ�������| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
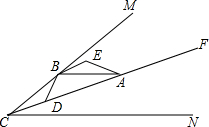 ��֪CAƽ�֡�MCN��AB��CN����D���߶�CA����һ�㣬��BD=BE����DBE=��CBA����AE��DE
��֪CAƽ�֡�MCN��AB��CN����D���߶�CA����һ�㣬��BD=BE����DBE=��CBA����AE��DE �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com