
【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论::①DE=DF,②AE=AF,③BD=CD,④AD⊥BC.其中正确的结论是 . (填序号) 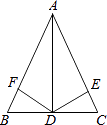
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国固有领土,位于我国东海,总面积约6340000平方米,数据6340000用科学记数法表示为( )
A.634×104
B.63.4×105
C.6.34×106
D.6.34×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x (元) | 15 | 20 | 25 | … |
y (件) | 25 | 20 | 15 | … |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:

(1)当AC>BC时,点D在线段 上; 当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10![]() ?
?
(3)若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图像. 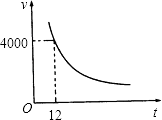
(1)请你根据图像提供的信息求出此蓄水池的蓄水量;
(2)求出此函数的解析式;
(3)若要6h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量不超过5 000m3 , 那么水池中的水至少要多少小时排完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)

(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,则点A表示的数是 。
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动的情况记录如下:+2,-1,-5,+4,+3,-2.
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动后,Q点运动的路程共有多少?此时点Q所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
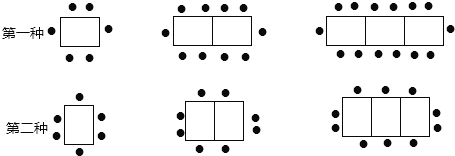
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人;
(2)当有n张桌子时,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人
(用含有n的代数式表示);
(3)一天中午,餐厅要接待85为顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com