
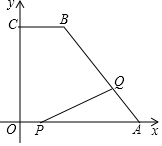
 如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:
如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:分析 (1)过点Q作QD⊥x轴于点D,利用勾股定理求出AB的长度,即可求证AO=AB;
(2)△APQ为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;
(3)①当PQ∥AB时,此时点Q只能在BC上,且易证四边形QBAP是平行四边形,利用平行四边形的性质即可求出点D的坐标.
②分点Q在AB上,Q在BC上讨论点D的坐标,从而求出点D运动的轨迹,进而求出D运动的距离.
解答 解:(1)过点Q作QD⊥x轴于点D,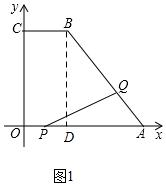
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
∴AB=AO;
(2)由题意可知:0≤t≤7,
当点P是直角顶点时,
∴PQ⊥AP,
∴PA=10-t,
若0≤t≤5时,点Q在AB上,如图2,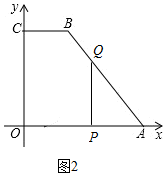
此时AQ=2t,
∵cos∠BAO=$\frac{3}{5}$,
∴$\frac{AP}{AQ}$=$\frac{3}{5}$,
∴t=$\frac{50}{11}$,
若5<t≤7时,点Q在BC上,如图3,
∴CQ=14-2t,OP=t,
∴OP=CQ,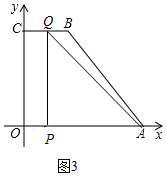
∴t=14-2t,
∴t=$\frac{14}{3}$,此情况不存在;
当点A是直角顶点时,
此时,∠QAP不可能为90°,此情况不符合题意;
当点Q是直角顶点时,
若0≤t≤5时,Q在AB上,如图4,
此时,AQ=2t,AP=10-t
∵cos∠BAO=$\frac{6}{10}$=$\frac{3}{5}$,
∴$\frac{AQ}{AP}$=$\frac{3}{5}$,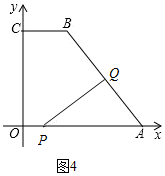
∴$\frac{2t}{10-t}$=$\frac{3}{5}$,
∴t=$\frac{30}{13}$,
若5<t≤7时,点Q在BC上,如图5,
过点Q作QE⊥x轴于点E,
此时,CQ=14-2t,OP=t,
QE=8,PE=CQ-OP=14-3t,
EA=10-(14-2t)=2t-4,
∵∠PQA=∠QEA=90°,
∴∠PQE+∠EQA=∠EQA+∠QAP=90°,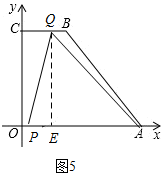
∴∠PQE=∠QAP,
∴△PQE∽△QAE,
∴$\frac{QE}{PE}=\frac{EA}{QE}$,
∴QE2=PE•EA,
∴64=(14-3t)(2t-4),
化简可得:3t2-8t+60=0,
△=-656<0,故此情况不存在;
综上所述,t=$\frac{50}{11}$或$\frac{30}{13}$;
(3)①当PQ∥AB时,如图6,
此时四边形QBAP是平行四边形,
∴PQ=AB=10,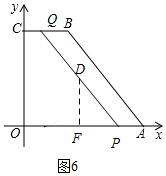 ∵点D是PQ的中点,
∵点D是PQ的中点,
∴PD=5,
过点D作DF⊥x轴于点F,
∴sin∠DPF=sin∠BAO=$\frac{4}{5}$,
∴$\frac{DF}{PD}$=$\frac{4}{5}$,
∴DF=4,
∴由勾股定理可知:PF=3,
∵QB=PA=2t-10,OP=t,
PA+OP=10,
∴2t-10+t=10,
∴t=$\frac{20}{3}$,
∴OF=$\frac{20}{3}$-3=$\frac{11}{3}$,
∴D的坐标为($\frac{11}{3}$,4)
②过点D作DF⊥x轴于点F,
当0≤t≤5时,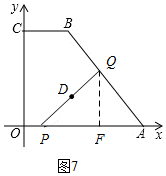 如图7,
如图7,
此时,OP=t,AQ=2t,
∵sin∠BAO=$\frac{4}{5}$,
∴$\frac{QF}{AQ}$=$\frac{4}{5}$,
∴QF=$\frac{8}{5}t$,
由勾股定理可知:AF=$\frac{6}{5}t$,
∴OF=10-$\frac{6}{5}$t,
∴点Q的坐标为(10-$\frac{6}{5}$t,$\frac{8}{5}t$),
∵P的坐标为(t,0),
∴由中点坐标公式可知:D的坐标为(5-$\frac{t}{10}$,$\frac{4}{5}$t)
∴点D在直线y=-8x+40上,
当t=0时,D的坐标为(5,0),
当t=5时,D的坐标为($\frac{9}{2}$,4),
∴由勾股定理可知:点D走过的路程为$\frac{\sqrt{65}}{2}$;
当5<t≤7时,如图8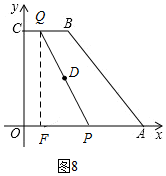
此时,OP=t,CQ=14-2t,
∴点P的坐标为(t,0),Q(14-2t,8),
∴由中点坐标公式可知:D的坐标为(7-$\frac{t}{2}$,4)
∴此时点D在直线y=4上,
当t=5时,D的坐标为($\frac{9}{2}$,4),
当t=7时,D的坐标为($\frac{7}{2}$,4),
∴D走过的路程为1,
∴D运动的距离为:1+$\frac{\sqrt{65}}{2}$
点评 本题考查三角形的综合问题,涉及平行四边形的判定与性质,相似三角形的判定与性质,锐角三角函数,解方程等知识,综合程度较高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 按下列要求画图并填空:
按下列要求画图并填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
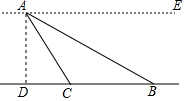 如图,一搜救船在海面A处测得亚航失事客机的第一个黑匣子的俯角∠EAC为60°,第二个黑匣子的俯角∠EAB为30°,此处海底的深度AD为3千米.求两个黑匣子的距离BC的长?(取$\sqrt{3}$≈1.73,精确到0.1千米)
如图,一搜救船在海面A处测得亚航失事客机的第一个黑匣子的俯角∠EAC为60°,第二个黑匣子的俯角∠EAB为30°,此处海底的深度AD为3千米.求两个黑匣子的距离BC的长?(取$\sqrt{3}$≈1.73,精确到0.1千米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
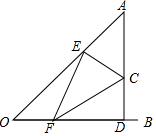 如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$.
如图,∠AOB=45°,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是9$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着科技的发展,无人机的应用越来越广泛,2016年7月14日多家记者用无人飞机航拍湖北第二大湖炸堤泄洪画面.如图,无人飞机从A处水平飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
随着科技的发展,无人机的应用越来越广泛,2016年7月14日多家记者用无人飞机航拍湖北第二大湖炸堤泄洪画面.如图,无人飞机从A处水平飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com